Simulation-based testing

# Simulation-based testing
## Part 1
### Prof. Maria Tackett

---

<div class="my-footer">
<span>
<a href="http://datasciencebox.org" target="_blank">datasciencebox.org</a>
</span>
</div>

---

## [Click for PDF of slides](11-sim-inference-pt1.pdf)

---

## Packages and set seed

```r
library(tidyverse)
library(infer)
```

```r
set.seed(0917)
```

---

## The hypothesis testing framework

---

## Parameter vs. statistic

A .vocab[parameter] for is the "true" value of interest. We typically estimate the 
parameter using a .vocab[sample statistic] as a point estimate.

Common population parameters of interest and their corresponding
sample statistic:

| Quantity           | Parameter  | Statistic   |
|--------------------|------------|-------------|
| Mean               | `$\mu$`      | `$\bar{x}$`   |
| Variance           | `$\sigma^2$` | `$s^2$`       |
| Standard deviation | `$\sigma$`   | `$s$`         |
| Proportion         | `$p$`        | `$\hat{p}$`   |

---

## How can we answer research questions using statistics?

.vocab[Statistical hypothesis testing] is the procedure that assesses
evidence provided by the data in favor of or against some claim
about the population (often about a population parameter or
potential associations).

---

## Motivating example: organ donors

People providing an organ for donation sometimes seek the help of a special 
medical consultant. These consultants assist the patient in all aspects of the 
surgery, with the goal of reducing the possibility of complications during the 
medical procedure and recovery. Patients might choose a consultant based in part 
on the historical complication rate of the consultant's clients.

One consultant tried to attract patients by noting that the **average complication 
rate for liver donor surgeries in the US is about 10%**, but **her clients have only 
had 3 complications in the 62 liver donor surgeries she has facilitated**. She 
claims this is strong evidence that her work meaningfully contributes to 
reducing complications (and therefore she should be hired!).

---

## Data

```r
organ_donor %>% 
  count(outcome)
```

```
## # A tibble: 2 x 2
##   outcome             n
##   <chr>           <int>
## 1 complication        3
## 2 no complication    59
```

---

## Organ donors: Parameter vs. statistic

**Parameter**, `$p~$`: true rate of complication

<br>

**Statistic**, `$\hat{p}~$`: rate of complication in the sample = `$\frac{3}{62}$` = 
0.048

---

## Correlation vs. causation

**No.** The claim is that there is a causal connection, but the data are 
observational. For example, maybe patients who can afford a medical consultant 
can afford better medical care, which can also lead to a lower complication 
rate.

While it is not possible to assess the causal claim, it is still possible to 
test for an association using these data.

For this question we ask, **how likely
is it that the low complication rate observed of `$\hat{p}$` = 0.048 be due solely
to chance?**

---

## Two claims

- .vocab[Null hypothesis:] "There is nothing going on"

Complication rate for this consultant is no different than the US average of 10%

- .vocab[Alternative hypothesis:] "There is something going on"

Complication rate for this consultant is **lower** than the US average of 10%

.question[
In statistical hypothesis testing we always first assume that the null 
hypothesis is true and then see whether we reject or fail to reject this claim. 
]

---

## Hypothesis testing as a court trial

- **Null hypothesis**, `$H_0$`: Defendant is innocent

- **Alternative hypothesis**, `$H_a$`: Defendant is guilty

- **Present the evidence:** Collect data

- **Judge the evidence:** "Could these data plausibly have happened by chance if the null hypothesis were true?"
    * Yes: Fail to reject `$H_0$`
    * No: Reject `$H_0$`
    
---

## The hypothesis testing framework

1️⃣ Start with two hypotheses about the population: the null hypothesis and the 
alternative hypothesis.

2️⃣ Choose a (representative) sample, collect data, and analyze the data.

3️⃣ Figure out how likely it is to see data like what we observed, IF the null 
hypothesis were in fact true (called a **p-value**)

4️⃣ If our data would have been extremely unlikely if the null hypothesis were true, 
then we reject it in favor of the alternative hypothesis.

Otherwise, we cannot reject the null hypothesis

---

## 1️⃣ Defining the hypotheses

Remember, the null and alternative hypotheses are defined for **parameters,**
not statistics

What will our null and alternative hypotheses be for this example?

- `$H_0$`: the true proportion of complications among her patients is **equal** to the 
US population rate
- `$H_a$`: the true proportion of complications among her patients is **lower** than
the US population rate

Expressed in symbols:

- `$H_0: p = 0.10$`
- `$H_a: p < 0.10$`
---

## 2️⃣ Collecting and summarizing data

With these two hypotheses, we now take our sample and summarize the data.

The choice of summary statistic calculated depends on the type of data. In our 
example, we use the sample proportion

`$$\hat{p} = 3/62 \approx 0.048$$`

---

## 3️⃣ Assessing the evidence observed

Next, we calculate the probability of getting data like ours, *or more extreme*, 
if `$H_0$` were in fact actually true.

This is a conditional probability: "given that `$H_0$` is true, `$p = 0.1$`, what would the the probability of observing `$\hat{p} = 3/62$` or less?"

<br>

This probability is known as the .vocab[p-value].

---

# Calculate the p-value using simulation

---

## Simulating the null distribution

Let's return to the organ transplant scenario.

Since `$H_0: p = 0.10$`, we need to simulate a distribution for `$\hat{p}$` under 
the null hypothesis such that the probability of complication for each patient 
is 0.10 for 62 patients.

This null distribution for `$\hat{p}$` represents the distribution of the observed 
proportions we might expect, if the null hypothesis were true.

.question[
When sampling from the null distribution, what is the expected proportion of
complications? 
]

---

## Data

```r
glimpse(organ_donor)
```

```
## Rows: 62
## Columns: 1
## $ outcome <chr> "complication", "complication", "complication", "no complicat…
```

```r
organ_donor %>%
  count(outcome)
```

```
## # A tibble: 2 x 2
##   outcome             n
##   <chr>           <int>
## 1 complication        3
## 2 no complication    59
```

---

## Simulation #1

```
## sim1
##    complication no complication 
##               3              59
```

```
## [1] 0.0483871
```

---

## Simulation #2

```
## sim2
##    complication no complication 
##               9              53
```

```
## [1] 0.1451613
```

---

## Simulation #3

```
## sim3
##    complication no complication 
##               8              54
```

```
## [1] 0.1290323
```

---

## This is getting boring...

We need a way to automate this process!
---

## Using infer to generate the null distribution

```r
null_dist <- organ_donor %>%
  specify(response = outcome, success = "complication") %>% 
  hypothesize(null = "point", 
              p = c("complication" = 0.10, "no complication" = 0.90) 
              ) %>% 
  generate(reps = 100, type = "simulate") %>% 
  calculate(stat = "prop")
```
]

---

## Specify

```r
null_dist <- organ_donor %>%
* specify(response = outcome, success = "complication") %>%
  hypothesize(null = "point", 
              p = c("complication" = 0.10, "no complication" = 0.90) 
              ) %>% 
  generate(reps = 100, type = "simulate") %>% 
  calculate(stat = "prop")
```
]

- .vocab[`response`]: **`outcome`** in the **`organ_donor`** data frame

- .vocab[`success`]: **`"complication"`**, the level of outcome we're interested in studying

---

## Hypothesize

```r
null_dist <- organ_donor %>%
  specify(response = outcome, success = "complication") %>% 
* hypothesize(null = "point",
*             p = c("complication" = 0.10, "no complication" = 0.90)
*             ) %>%
  generate(reps = 100, type = "simulate") %>% 
  calculate(stat = "prop")
```
]

- .vocab[`null`]: Since we're testing the point null hypothesis that `$H_0: p = 0.10$`, we
choose **`"point"`**
- Next, we provide the probability of "success" and "failure"
  - **`"complication" = 0.10, "no complication" = 0.90`**

---

## Generate

```r
null_dist <- organ_donor %>%
  specify(response = outcome, success = "complication") %>% 
  hypothesize(null = "point", 
              p = c("complication" = 0.10, "no complication" = 0.90) 
              ) %>% 
* generate(reps = 100, type = "simulate") %>%
  calculate(stat = "prop")
```
]

- .vocab[`reps`]: We will generate 100 repetitions here
- .vocab[`type`]: Choose **`"simulate"`** for testing a point null for categorical data
    - Choose `bootstrap` for estimation 
    - Choose `permute` for testing independence 
---

## Calculate

- Calculate a sample statistic. Here, the sample proportion.
  - `stat = "prop"`

---

## Store simulated null distribution

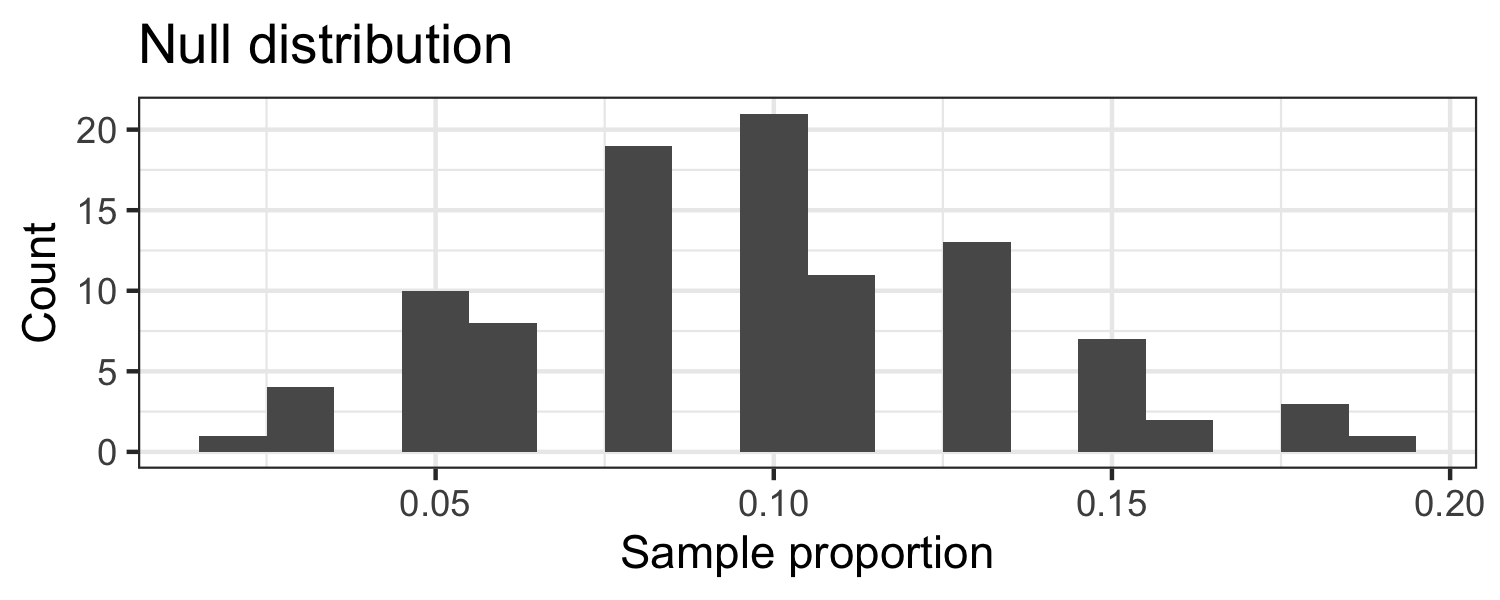
```r
*null_dist <- organ_donor %>%
  specify(response = outcome, success = "complication") %>% 
  hypothesize(null = "point", 
              p = c("complication" = 0.10, "no complication" = 0.90) 
              ) %>% 
  generate(reps = 100, type = "simulate") %>%  
  calculate(stat = "prop") 
```
]

```
## # A tibble: 100 x 2
##    replicate  stat
##        <dbl> <dbl>
##  1         1 0.048
##  2         2 0.097
##  3         3 0.081
##  4         4 0.081
##  5         5 0.161
##  6         6 0.081
##  7         7 0.081
##  8         8 0.032
##  9         9 0.113
## 10        10 0.113
## # … with 90 more rows
```

---

## Visualizing the null distribution

---

## Calculating the p-value, visually

---

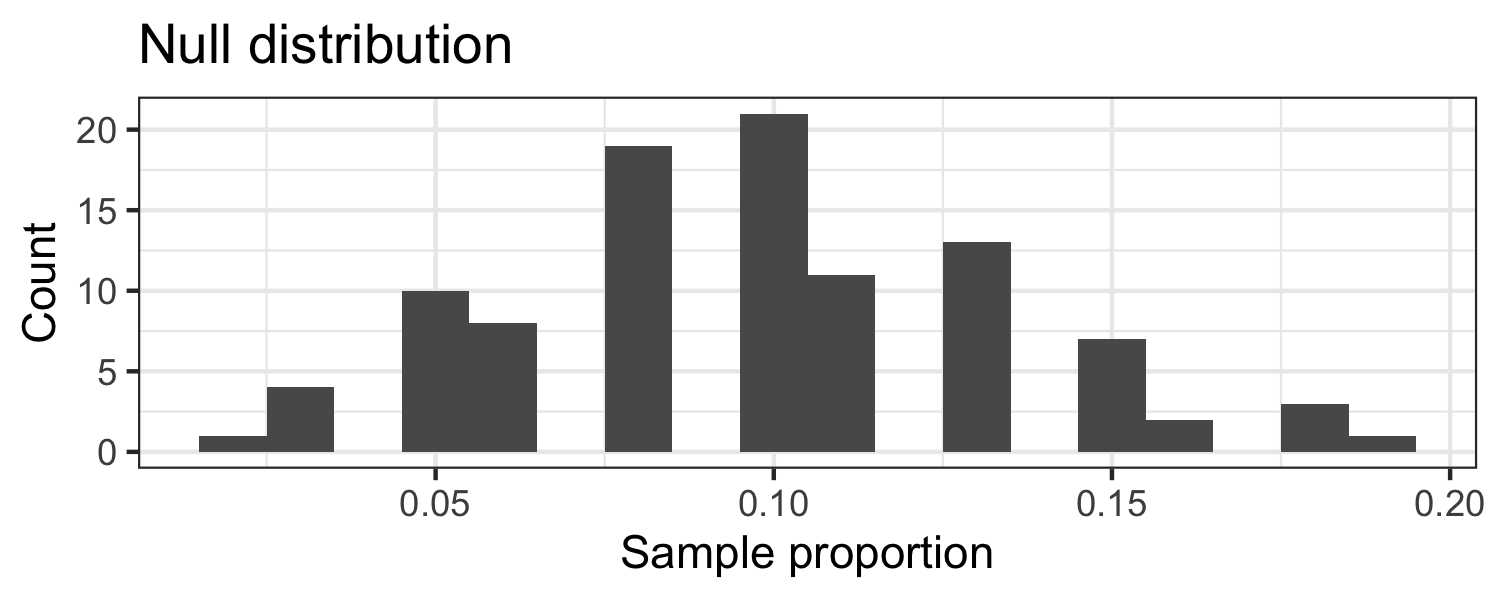
## Calculating the p-value, directly

```r
null_dist %>%
  filter(stat <= (3/62)) %>%
  summarise(p_value = n()/nrow(null_dist))
```

```
## # A tibble: 1 x 1
##   p_value
##     <dbl>
## 1    0.15
```

---

## 4️⃣ Making a conclusion

We reject the null hypothesis if the p-value is probability is small enough, i.e. it is very unlikely to observe our data or more extreme if `$H_0$` were 
actually true.

What is "small enough"? We often consider a threshold (the .vocab[significance level]
or `$\alpha$`-level) defined *prior* to conducting the analysis.

---

## Significance level

We often use 5% as the cutoff for whether the p-value is low enough that the data are unlikely to have come from the null model.

- If p-value < `$\alpha$`, reject `$H_0$` in favor of `$H_a$`:     
  - The data provide convincing 
evidence against the null hypothesis

- If p-value  `$\geq \alpha$`, fail to reject `$H_0$` in favor of `$H_a$`
  - The data do not provide 
convincing evidence against the null hypothesis.

---

## What if `$p$`-value  `$\geq \alpha$`?

If p-value `$\geq \alpha$` we fail to reject `$H_0$`.

Importantly, we never "accept" the null hypothesis.

When we fail to reject the null hypothesis, we are stating that there is 
**insufficient evidence** to conclude that it is false. This could be due to any 
number of reasons:

- There truly is no effect
- There truly is an effect (and we happened to get unlucky with our sample or 
didn't have enough data to tell that there was one)

---

## Organ donor example

The p-value 0.15 is greater than the significance level, `$\alpha = 0.05$`, so we .vocab[fail to reject the null hypothesis].

The data .vocab[do not] provide sufficient evidence that the true complication rate for this consultant's clients is less than the US rate, `$p = 0.1$`.