Two-sample inference

# Two-sample inference
### Prof. Maria Tackett

---

<div class="my-footer">
<span>
<a href="http://datasciencebox.org" target="_blank">datasciencebox.org</a>
</span>
</div>

---

## [Click for PDF of slides](15-two-samp-inference.pdf)

---

## Recap

So far, we've talked about performing interval estimation and hypothesis 
testing for means using

- simulation-based methods, such as bootstrap or direct simulation, and
- the Central Limit Theorem

In all cases so far, we've only compared one sample against a hypothesized 
value.

---

## Two-sample inference for means

Suppose we have two (representative)
samples, and wanted to either

- estimate the .vocab[difference in means] in the two
populations 
  - confidence interval for `\(\mu_1 - \mu_2\)`
  
- Test the hypotheses

`\begin{align*}
H_0: \mu_1 = \mu_2 \\
H_a: \mu_1 \neq \mu_2,
\end{align*}`

where `\(\mu_1\)` and `\(\mu_2\)` are the population means in groups 1 and 2.

---

.question[
How might you calculate a confidence interval and address the above hypothesis test using simulation-based methods? How about the CLT?
]

---

## Today's data

.footnote[Adapted from Erdogdu Sakar, B., et al. *Collection and Analysis of a Parkinson*
*Speech Dataset with Multiple Types of Sound Recordings*, IEEE Journal of 
Biomedical and Health Informatics, vol. 17(4), pp. 828-834, 2013
(image from [Wikipedia](https://en.wikipedia.org/wiki/Spectrogram))]

---

## Some voice analysis terminology

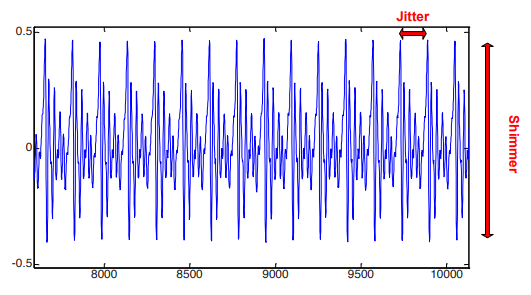
- .vocab[Jitter]: frequency variation from cycle to cycle
- .vocab[Shimmer]: amplitude variation of the sound wave

Jitter and shimmer are affected by lack of control of vocal cord vibration, and
pathological differences from average values may be indicative of Parkinson's
Disease (PD).

(from Teixeira, Oliveira, and Lopes, 2013)

---

## Question of interest

Is there a difference in average voice jitter between patients with Parkinson's disease (PD) and those who don't have Parkinson's disease (control group)?

`parkinsons.csv` contains repeated voice recordings from a number of patients,
some with PD and some serving as non-PD controls (Erdogdu B et al.). For now,
**assume that all samples were taken independently from each other** (this is
not actually the case, but we'll make this assumption).

Jitter is given in milliseconds (ms), and shimmer is given in decibels (dB).

---

## Bootstrap estimation

Let's construct the bootstrap distribution for the **difference in means**.

```r
set.seed(2020)
parkinsons <- read_csv("data/parkinsons.csv")

library(infer)

boot_diffs <- parkinsons %>% 
* specify(jitter ~ status) %>%
  generate(reps = 1000, type = "bootstrap") %>% 
* calculate(stat = "diff in means",
*           order = c("Healthy", "PD"))
```

---

## Bootstrap estimation

Let's construct the bootstrap distribution for the *difference* in means.

---

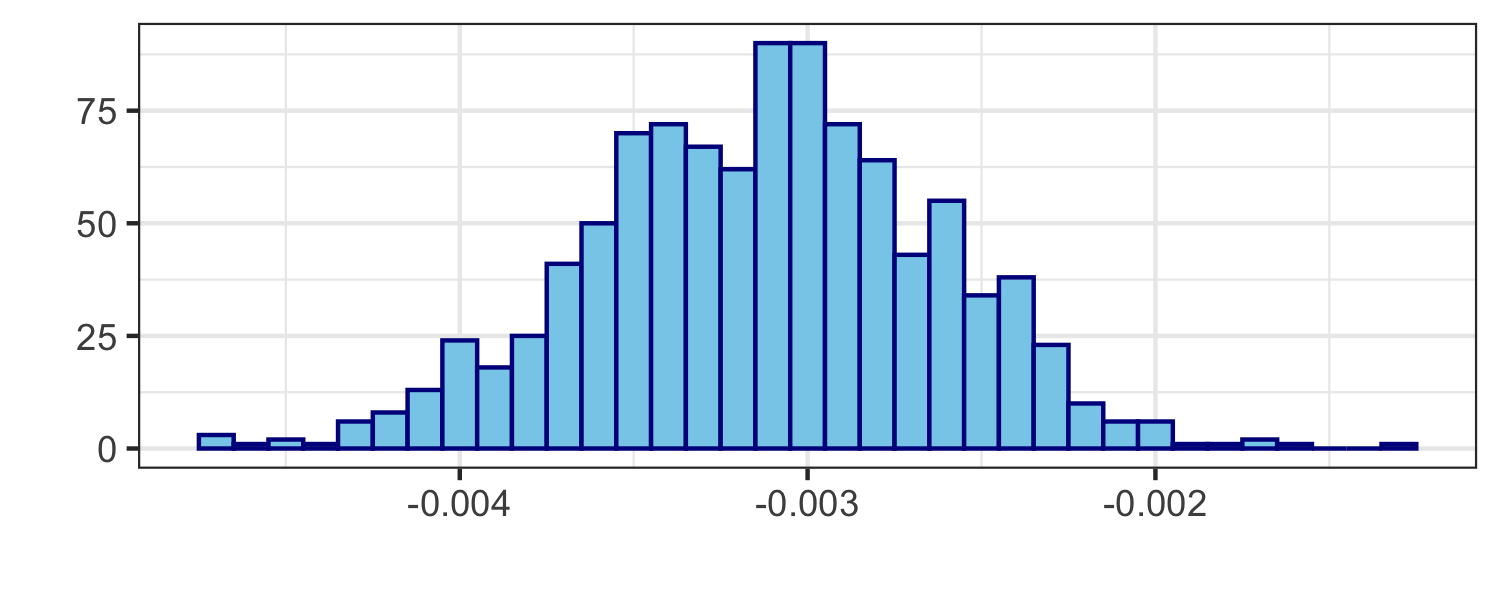
## CI for difference in means

Let's construct the bootstrap distribution for the **difference in means**.

```r
boot_diffs %>% 
  summarize(lower = quantile(stat, 0.025),
            upper = quantile(stat, 0.975))
```

```
## # A tibble: 1 x 2
##      lower    upper
##      <dbl>    <dbl>
## 1 -0.00413 -0.00220
```

---

## CI for difference in means

```
## # A tibble: 1 x 2
##      lower    upper
##      <dbl>    <dbl>
## 1 -0.00413 -0.00220
```

.vocab[Interpretation: ]We are 95% confident that the mean voice jitter for people without Parkinson's disease is about 0.002 to 0.004 ms less than the mean voice jitter for those with Parkinson's disease.

.question[
Is there evidence that there is a difference in mean voice jitter between PD patients and healthy patients?
]

---

## Hypothesis testing

Let `\(\mu_P\)` be the mean voice jitter among PD patients, and `\(\mu_H\)` be the mean
voice jitter among healthy patients. Let's test

`\begin{align*}
H_0: \mu_P = \mu_H\\
H_a: \mu_P \neq \mu_H
\end{align*}`

If the two means are truly equal (i.e., if `\(H_0\)` is true), then the difference, `\(\mu_H - \mu_P\)`, should be **zero**.

---

## Hypothesis testing

Let's construct the simulated .vocab[null distribution] for the difference in means, `\(\mu_H - \mu_P\)`. If the two means are truly equal (i.e., if `\(H_0\)` is true), then this difference should be zero.

```r
null_dist <- parkinsons %>%
  specify(jitter ~ status) %>%
* hypothesize(null = "independence") %>%
* generate(reps = 1000, type = "permute") %>%
  calculate(stat = "diff in means", 
*           order = c("Healthy", "PD"))
```

---

## Hypothesis testing
  
<img src="15-two-samp-inference_files/figure-html/unnamed-chunk-8-1.png" style="display: block; margin: auto;" />

---

## Hypothesis testing

```r
obs_diff <- parkinsons %>% 
  specify(jitter ~ status) %>% 
  calculate(stat = "diff in means", order = c("Healthy", "PD")) %>% 
  pull()
obs_diff
```

```
## [1] -0.00312321
```

```r
null_dist %>% 
  filter(abs(stat) >= abs(obs_diff)) %>%
  summarise(p_val = n() / nrow(null_dist))
```

```
## # A tibble: 1 x 1
##   p_val
##   <dbl>
## 1     0
```

---

## Conclusion

The p-value is very small, so we reject `\(H_0\)`. The data provide sufficient evidence that there is a difference in the mean voice jitter between patients who have Parkinson's disease and those who don't have the disease.

---

## Difference in means using CLT
--

CLT-based inference for a difference in means relies on the 
.vocab[two-sample t-test for independent samples]. Like the t-test we've seen
before, the **test statistic** takes on the following form:

`\begin{align*}
T = \frac{(\bar{X}_1 - \bar{X}_2) - (\mu_1 - \mu_2) }{\widehat{SE}_{diff}}
\end{align*}`

The test statistic depends on whether we can assume that the two groups have the 
same underlying variability in their observations.

The exact form of the test statistic under the null hypothesis, including the
degrees of freedom, are a complicated fraction that no one calculates by hand. Let's let R handle this!

---

## CLT: Difference in means

```r
parkinsons %>%
  t_test(jitter ~ status, 
         mu = 0,
         order = c("Healthy", "PD"), 
         alternative = "two-sided", 
         conf_int = TRUE, conf_level = 0.95)
```

```
## # A tibble: 1 x 6
##   statistic  t_df      p_value alternative lower_ci upper_ci
##       <dbl> <dbl>        <dbl> <chr>          <dbl>    <dbl>
## 1     -5.96  187. 0.0000000124 two.sided   -0.00416 -0.00209
```

---

## CLT: Difference in means

.question[
Comprehensively evaluate the research question by specifying the hypotheses, 
the test statistic and its the distribution under the null, the p-value,
and decision at the `\(\alpha = 0.05\)` significance level. Interpret the 
conclusions from your hypothesis test in context of the original research 
question.
]