Comparing three or more groups

class: center, middle, inverse, title-slide

# Comparing three or more groups
### Prof. Maria Tackett

---

class: middle center

## [Click for PDF of slides](16-chi-sq.pdf)
---

## An old example...

| Coffee             | Died  | Did not die  |
| ------------------ |------:| ------------:|
| Non-drinker        | 1039  | 5438         |
| Occasional drinker | 4440  | 29712        |
| Regular drinker    | 3601  | 24934        |

We have more than two samples! Non-coffee drinkers, occasional drinkers, and
regular drinkers.

.vocab[
Is there an *association* between coffee drinking *status* and whether somebody
died? Are the two **independent**?
]

---

## A new hypothesis test...

- `\(H_0\)`: Coffee-drinking category and health outcome are independent; there is no
association between the two variables
- `\(H_a\)`: Coffee-drinking category and health outcome are NOT independent; there is
an association between the two variables

---

## Review

If `\(H_0\)` were true, then we would expect:
- .midi[P(Non-Drinker) x P(Died) = P(Non-drinker AND Died)]
--

- .midi[P(Occasional Drinker) x P(Died) = P(Occasional drinker AND Died)]
--

- .midi[P(Regular Drinker) x P(Died) = P(Regular drinker AND Died)]
--

- .midi[P(Non-Drinker) x P(Lived) = P(Non-drinker AND Lived)]
--

- .midi[P(Occasional Drinker) x P(Lived) = P(Occasional drinker AND Lived)]
--

- .midi[P(Regular Drinker) x P(Lived) = P(Regular drinker AND Lived)]

---

## Observed vs. expected counts

Let's investigate non-coffee drinking and dying:

- P(Non-Drinker) = 6477/69164 `\(\approx\)` 0.09365
- P(Died) = 9080/69164 `\(\approx\)` 0.131

If these were independent, we would *expect* P(Non-Drinker AND Died) to be
6477/69164 `\(\times\)` 9080/69164 `\(\approx\)` 0.012. So, we expect approximately 
850 study participants to be non-drinkers who died.

---

## Observed vs. expected counts

The **observed** number is 1039, for a difference of 189 participants between
the observed and expected counts.

.question[
Is this strong evidence against the claim of independence?
]

---

## Observed vs. expected counts

Well, that was just one cell! There are five more cells in which there may be differences between observed and expected counts.

.question[
How can we sum up these differences in a principled way, and use it to conduct statistical inference?
]

---

## The chi-square test

The .vocab[chi-squared test] has a very nice motivation in terms of comparing observed vs. the expected counts that we would expect if `\(H_0\)` were true.

If these total differences are **"large enough,"** then we **reject** the null hypothesis.

- To combine differences across table cells, we need to square them before adding 
them up (so that
negative differences aren't canceled out by positive differences)

- We will also scale these differences by the expected count (a difference of 189 participants isn't large when thinking about 100,000 total observations, but is huge when thinking about 300 total observations!)

---

## The chi-square test statistic

The chi-square `\(\chi^2\)` test statistic is

`\begin{align*}
\sum_{i \in {cells}}^{r \times c} \frac{(O_i - E_i)^2}{E_i},
\end{align*}`

where `\(r \times c\)` is the number of cells in the table (rows times columns), `\(i\)` indexes across all cells, `\(O_i\)` is the expected count in cell `\(i\)`, and `\(E_i\)` is the expected count in cell `\(i\)`.

This statistic is the total squared difference between the observed and expected cell counts, scaling by the expected cell count for each cell.

Under `\(H_0\)`, the distribution of this sum is approximated by a `\(\chi^2\)` distribution with `\((r - 1) \times (c - 1)\)` degrees of freedom.

---

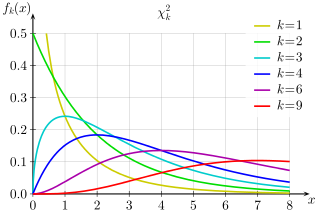
## Chi-squared distributions

Remember, we only reject if the difference is "large enough." So, we only examine the .vocab[right-tail]. That is, the probability of seeing our `\(\chi^2\)` statistic **or larger** when calculating p-values.

---

## Implementation in R

Luckily, you don't have to calculate all the expected counts by hand, create the test statistic, and manually compare to a chi-square distribution.

```r
coffee_data %>%
  slice(1:10)
```

```
## # A tibble: 10 x 2
##    coffee                health_outcome
##    <chr>                 <chr>         
##  1 Does not drink coffee Died          
##  2 Does not drink coffee Died          
##  3 Does not drink coffee Died          
##  4 Does not drink coffee Died          
##  5 Does not drink coffee Died          
##  6 Does not drink coffee Died          
##  7 Does not drink coffee Died          
##  8 Does not drink coffee Died          
##  9 Does not drink coffee Died          
## 10 Does not drink coffee Died
```

---

## Chi-square test using infer

```r
coffee_data %>%
  chisq_test(formula = health_outcome ~ coffee)
```

```
## # A tibble: 1 x 3
##   statistic chisq_df  p_value
##       <dbl>    <int>    <dbl>
## 1      55.2        2 1.05e-12
```

.question[
Formally assess the hypothesis that coffee drinking and health outcome are independent.

What might we conclude given these data? 
]