Is yawning contagious?

Is yawning contagious?

An experiment conducted by the MythBusters tested if a person can be subconsciously influenced into yawning if another person near them yawns.

Study description

In this study 50 people were randomly assigned to two groups: 34 to a group where a person near them yawned (treatment) and 16 to a control group where they didn't see someone yawn (control).

yawn %>% #in the openintro package
  count(group, result)

## # A tibble: 4 x 3
##   group result       n
##   <fct> <fct>    <int>
## 1 ctrl  not yawn    12
## 2 ctrl  yawn         4
## 3 trmt  not yawn    24
## 4 trmt  yawn        10

Proportion of yawners

yawn %>%
  count(group, result) %>%
  group_by(group) %>%
  mutate(p_hat = n / sum(n))

## # A tibble: 4 x 4
## # Groups:   group [2]
##   group result       n p_hat
##   <fct> <fct>    <int> <dbl>
## 1 ctrl  not yawn    12 0.75 
## 2 ctrl  yawn         4 0.25 
## 3 trmt  not yawn    24 0.706
## 4 trmt  yawn        10 0.294

• Proportion of yawners in the treatment group: 1034=0.2941

• Proportion of yawners in the control group: 416=0.25

• Difference: 0.2941−0.25=0.0441

Independence?

## # A tibble: 4 x 4
## # Groups:   group [2]
##   group result       n p_hat
##   <fct> <fct>    <int> <dbl>
## 1 ctrl  not yawn    12 0.75 
## 2 ctrl  yawn         4 0.25 
## 3 trmt  not yawn    24 0.706
## 4 trmt  yawn        10 0.294

Dependence, or another possible explanation?

• The observed differences might suggest that yawning is contagious, i.e. seeing someone yawn and yawning are dependent.

• But the differences are small enough that we might wonder if they might simple be due to chance.

• Perhaps if we were to repeat the experiment, we would see slightly different results.

• So we will do just that - well, somewhat - and see what happens.

• Instead of actually conducting the experiment many times, we will simulate our results.

Two competing claims

• "There is nothing going on." Yawning and seeing someone yawn are independent, yawning is not contagious, observed difference in proportions is simply due to chance. → Null hypothesis

• "There is something going on." Yawning and seeing someone yawn are dependent, yawning is contagious (i.e., seeing someone yawn makes you more likely to yawn), and observed difference in proportions is not due to chance. → Alternative hypothesis

Let's simulate the null distribution...

set.seed(102020)
null_dist <- yawn %>%
  specify(result ~ group, success = "yawn") %>%
  hypothesize(null = "independence") %>%
  generate(reps  = 1000, type = "permute") %>%
  calculate(stat = "diff in props", order = c("trmt", "ctrl"))

Let's simulate the null distribution...

set.seed(102020)
null_dist <- yawn %>%
  specify(result ~ group, success = "yawn") %>%
  hypothesize(null = "independence") %>% 
  generate(reps  = 1000, type = "permute") %>% 
  calculate(stat = "diff in props", order = c("trmt", "ctrl"))

Let's simulate the null distribution...

set.seed(102020)  
null_dist <- yawn %>% 
  specify(result ~ group, success = "yawn") %>%
  hypothesize(null = "independence") %>% 
  generate(reps  = 1000, type = "permute") %>% 
  calculate(stat = "diff in props", order = c("trmt", "ctrl"))

Let's simulate the null distribution...

set.seed(102020)  
null_dist <- yawn %>% 
  specify(result ~ group, success = "yawn") %>%
  hypothesize(null = "independence") %>%
  generate(reps  = 1000, type = "permute") %>% 
  calculate(stat = "diff in props", order = c("trmt", "ctrl"))

Let's simulate the null distribution...

set.seed(102020)  
null_dist <- yawn %>% 
  specify(result ~ group, success = "yawn") %>%
  hypothesize(null = "independence") %>% 
  generate(reps  = 1000, type = "permute") %>%
  calculate(stat = "diff in props", order = c("trmt", "ctrl"))

Let's simulate the null distribution...

set.seed(102020)  
null_dist <- yawn %>% 
  specify(result ~ group, success = "yawn") %>%
  hypothesize(null = "independence") %>% 
  generate(reps  = 1000, type = "permute") %>% 
  calculate(stat = "diff in props", order = c("trmt", "ctrl"))

Permuting yawn data

Remember, under H0, there is no association between yawning and seeing someone else yawn (i.e. control vs. treatment group.)

If there truly is no association, then shuffling whether someone was in the control or treatment group wouldn't matter -- we would expect similar proportions of people who yawn in each experimental group.

We will do this shuffling again and again, calculate the difference in proportion for each simulation, and use this as an approximation to the null distribution.

Permuting yawn data

This distribution approximates all the possible differences in proportion we could have seen if H0 were in fact true.

We then use this distribution to obtain the probability that we see our observed data (or more extreme) -- the p-value.

Here we sample without replacement; we merely permute the treatment labels of each of our outcomes.

Visualizing the null distribution

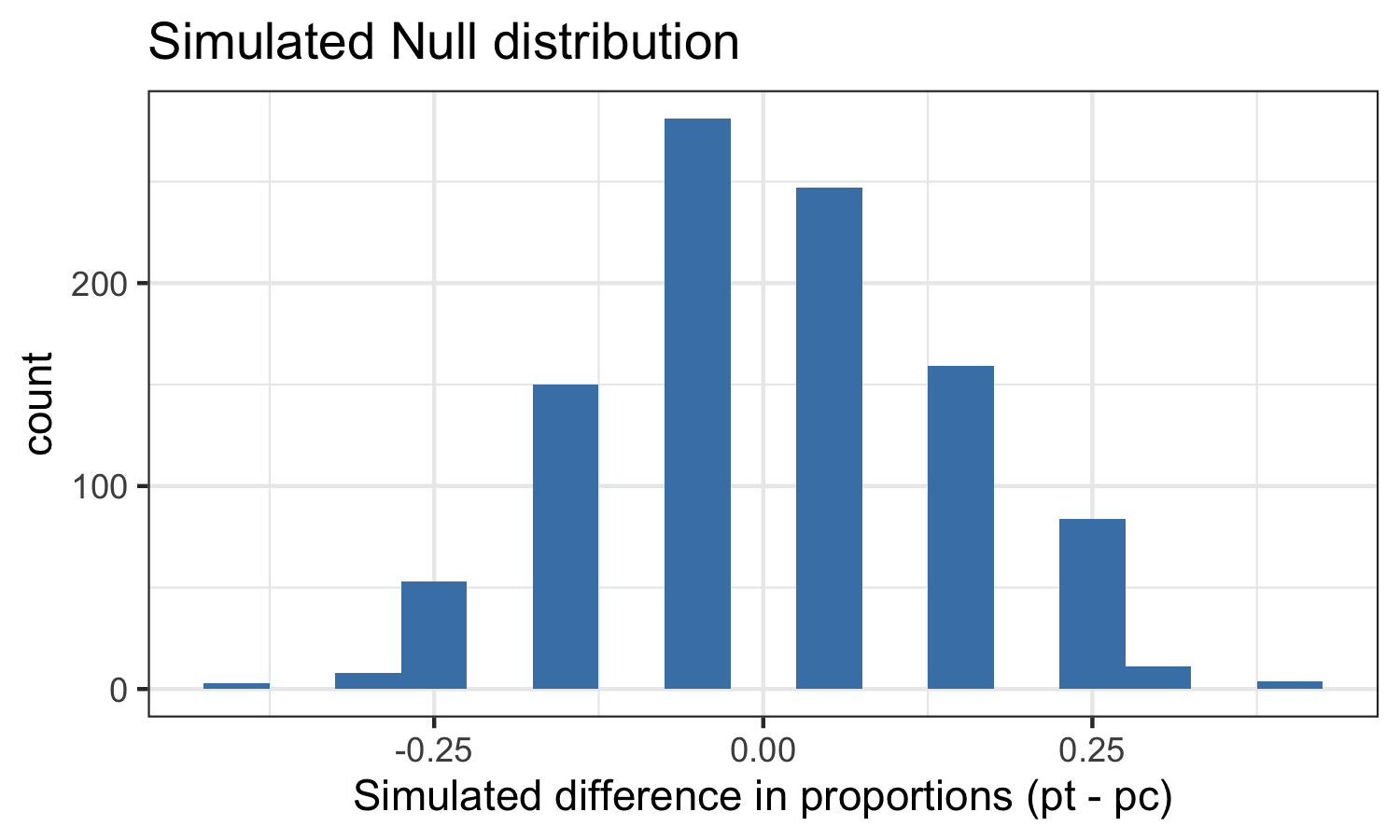
Calculating the p-value

null_dist %>%
  filter(stat >= 0.0441) %>%
  summarise(p_value = n()/nrow(null_dist))

## # A tibble: 1 x 1
##   p_value
##     <dbl>
## 1   0.505

Conclusion