Simulation-based testing

# Simulation-based testing
## Part 2
### Prof. Maria Tackett

---

<div class="my-footer">
<span>
<a href="http://datasciencebox.org" target="_blank">datasciencebox.org</a>
</span>
</div>

---

## [Click for PDF of slides](12-sim-inference-pt2.pdf)

---

## Terminology

- .vocab[Population]: a group of individuals or objects we are interested in studying

- .vocab[Parameter]: a numerical quantity derived from the population
(almost always unknown)

- .vocab[Statistical inference] is the process of using sample data to make 
  conclusions about the underlying population the sample came from.

- .vocab[Testing]: evaluating whether our observed sample provides evidence 
for or against some claim about the population

---

## The hypothesis testing framework

1️⃣ Start with two hypotheses about the population: the null hypothesis and the 
alternative hypothesis.

2️⃣ Choose a (representative) sample, collect data, and analyze the data.

3️⃣ Figure out how likely it is to see data like what we observed, IF the null 
hypothesis were in fact true (called a **p-value**)

4️⃣ If our data would have been extremely unlikely if the null hypothesis were true, 
then we reject it in favor of the alternative hypothesis.

Otherwise, we cannot reject the null hypothesis

---

## What can go wrong?

Suppose we test a certain null hypothesis, which can be either true or false
(we never know for sure!). We make one of two decisions given our data: either
reject or fail to reject `$H_0$`.

We have the following four scenarios:

| Decision             | `$H_0$` is true | `$H_0$` is false |
|----------------------|---------------|----------------|
| Fail to reject `$H_0$` | Correct decision    | **Type II Error** |
| Reject `$H_0$`         | **Type I Error**  | Correct decision     |

It is important to weigh the consequences of making each type of error.

---

## What can go wrong?

- `$\alpha$` is the probability of making a Type I error.

- `$\beta$` is the probability of making a Type II error.

- The .vocab[power] of a test is 1 - `$\beta$`: the probability that, if the null
hypothesis is actually false, we correctly reject it.

Though we'd like to know if we're making a correct decision or making a Type I or Type II error, hypothesis testing does **NOT** give us the tools to determine this.

---

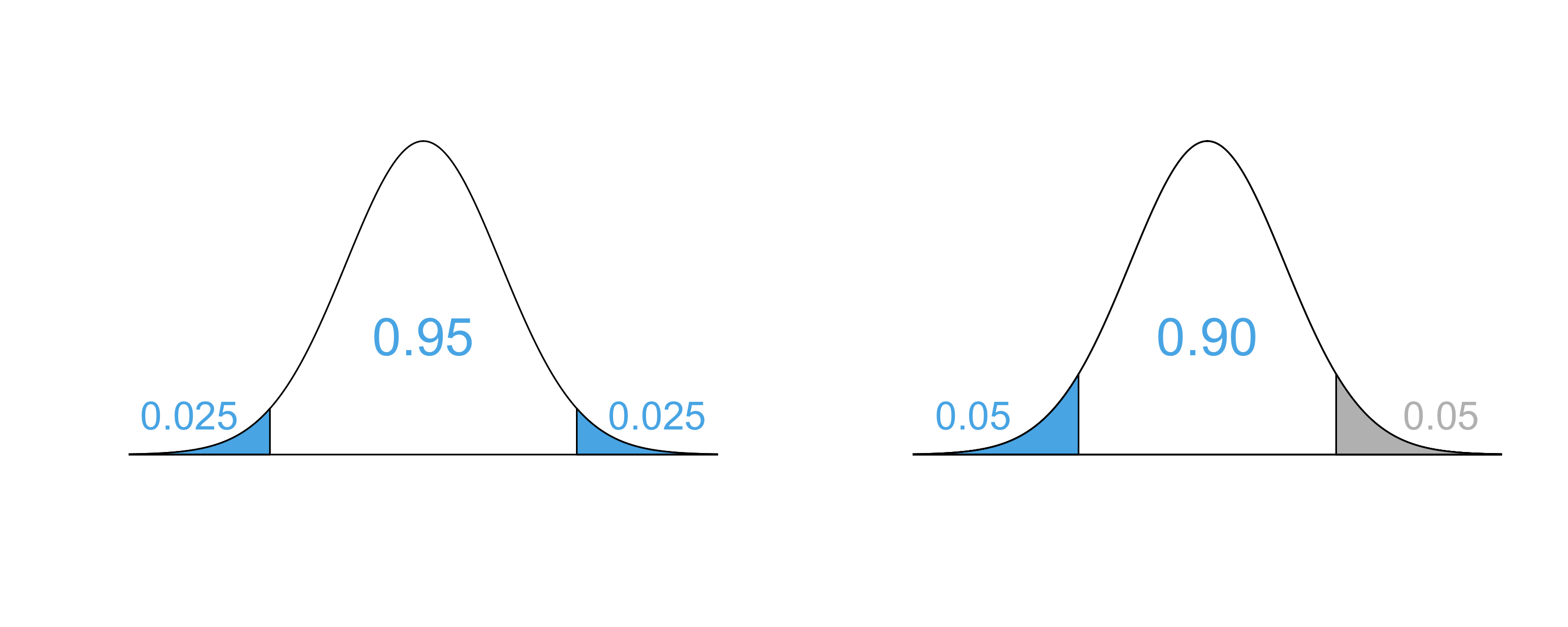
## Equivalency of confidence and significance levels

- Two sided alternative hypothesis test with `$\alpha$` `$\rightarrow$` `$CL = 1 - \alpha$`

- One sided alternative hypothesis with `$\alpha$` `$\rightarrow$` `$CL = 1 - (2 \times \alpha)$`

---

## Back to Asheville!

Your friend claims that the mean price per guest per night for Airbnbs in
Asheville is $100. **What do you make of this statement?**

Let's use hypothesis testing to assess this claim!

---

## 1️⃣ Defining the hypotheses

Remember, the null and alternative hypotheses are defined for **parameters,**
not statistics

- `$H_0$`: the true mean price per guest is $100 per night
- `$H_a$`: the true mean price per guest is NOT $100 per night

Expressed in symbols:

- `$H_0: \mu = 100$`
- `$H_a: \mu \neq 100$`

---

## 2️⃣ Collecting and summarizing data

With these two hypotheses, we now take our sample and summarize the data.

The choice of summary statistic calculated depends on the type of data. In our 
example, we use the sample mean: `$\bar{x} = 76.6$`:

```r
asheville <- read_csv("data/asheville.csv")

asheville %>% 
  summarize(mean_price = mean(ppg))
```

```
## # A tibble: 1 x 1
##   mean_price
##        <dbl>
## 1       76.6
```

---

## 3️⃣ Assessing the evidence

Next, we calculate the probability of getting data like ours, *<u>or more extreme</u>*, 
if `$H_0$` were in fact actually true.

This is a conditional probability: 
> Given that `$H_0$` is true (i.e., if `$\mu$` were *actually* 100), what would 
> be the probability of observing `$\bar{x} = 76.6$` or more extreme?

---

## Simulating the null distribution

Let's return to the Asheville data. We know that our sample mean was 76.6, but
we also know that if we were to take another random sample of size 50 from all
Airbnb listings, we might get a different sample mean.

There is some variability in the .vocab[sampling distribution] of the mean, and
we want to make sure we quantify this.

.question[
How might we quantify the sampling distribution of the mean using only the data
that we have from our original sample?
]

---
## Simulating the null distribution

There is some variability in the .vocab[sampling distribution] of the mean, and
we want to make sure we quantify this.

.question[
How might we quantify the sampling distribution of the mean using only the data
that we have from our original sample?
]

---

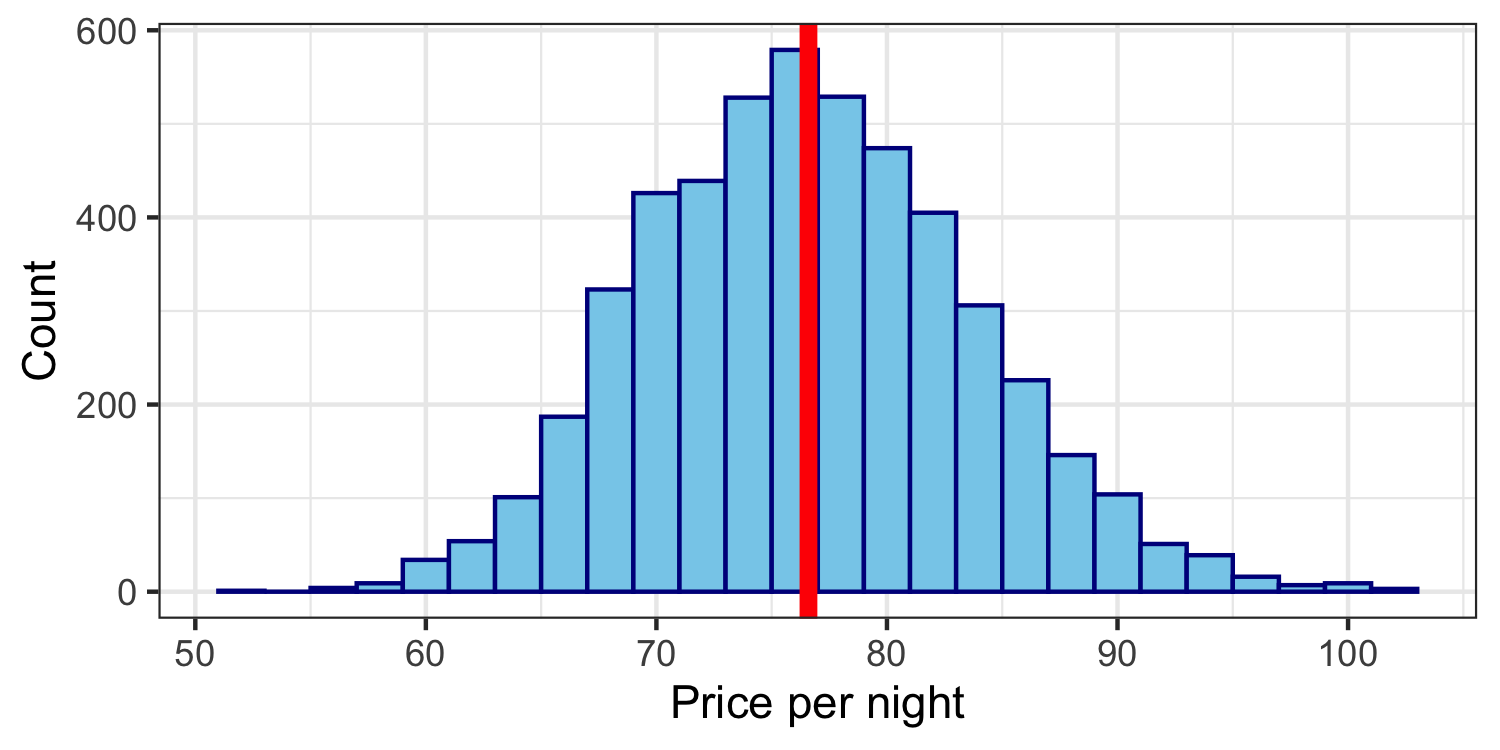
## Bootstrap distribution of the mean

```r
set.seed(12345)
library(infer)

boot_means <- asheville %>% 
* specify(response = ppg) %>%
* generate(reps = 5000, type =  "bootstrap") %>%
* calculate(stat = "mean")
```

```r
ggplot(data = boot_means, aes(stat)) +
  geom_histogram(binwidth = 2, color = "darkblue", fill = "skyblue") + 
  labs(x = "Price per night", y = "Count") +
  geom_vline(xintercept = mean(boot_means$stat), 
             lwd = 2, color = "red")
```

---

## Bootstrap distribution of the mean

---

## Shifting the distribution

We've captured the variability in the sample mean among samples of size 50 from
Asheville area Airbnbs, but remember that in the hypothesis testing paradigm,
we must assess our observed evidence under the assumption that the null 
hypothesis is true.

```r
boot_means %>% 
  summarize(mean(stat))
```

```
## # A tibble: 1 x 1
##   `mean(stat)`
##          <dbl>
## 1         76.6
```
]

`$H_0: \mu = 100$`

`$H_a: \mu \neq 100$`
]

---

.question[
Where should the bootstrap distribution of means be centered if in fact `$H_0$` 
were actually true?
]

---

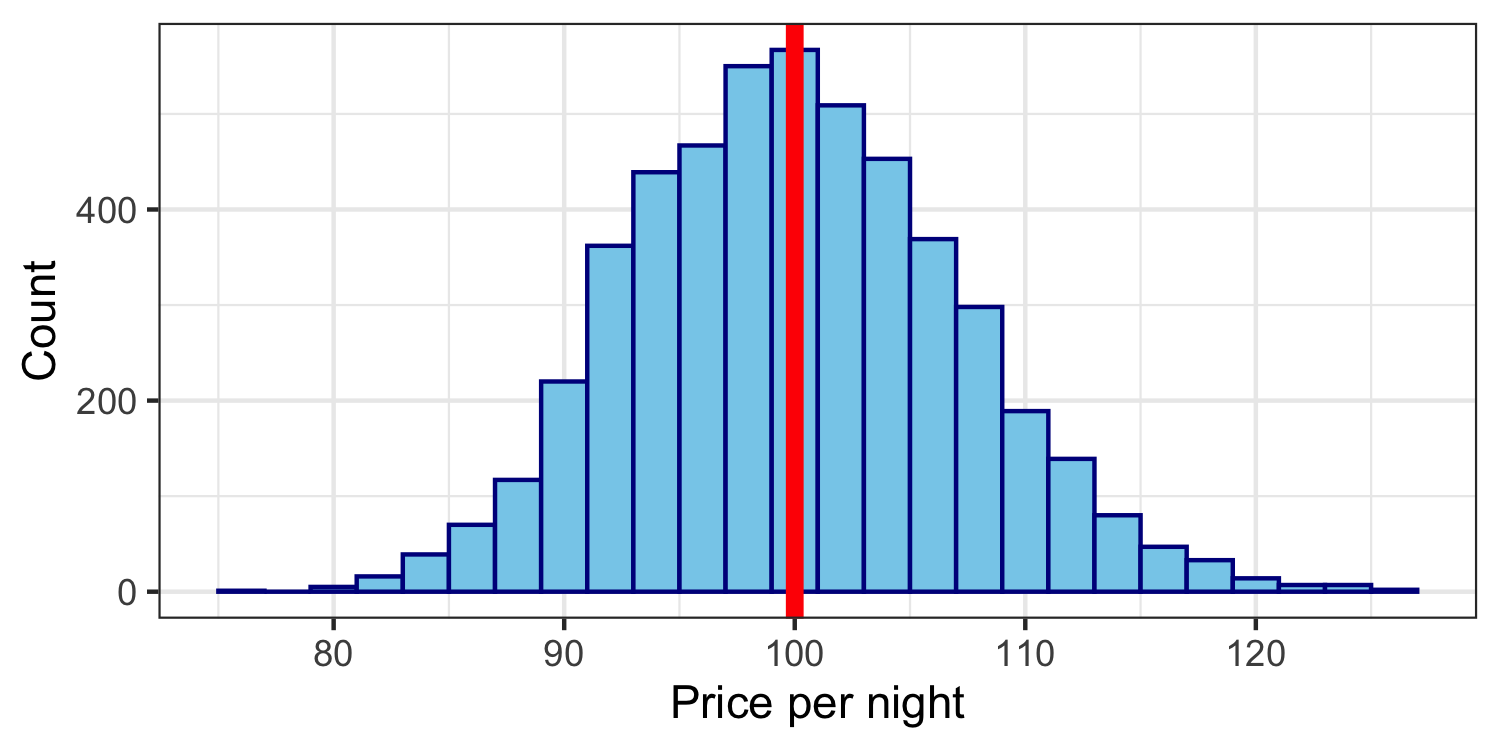
## Shifting the distribution

```r
ash_boot_mean <- boot_means %>% 
  summarize(mean = mean(stat)) %>% 
  pull()

*boot_means <- boot_means %>%
* mutate(null_dist_stat = stat - (ash_boot_mean - 100))
```

If we shifted the bootstrap distribution by `offset`, then it will be centered
at `$\mu_0$`: the null-hypothesized value for the mean.

```r
*ggplot(data = boot_means, aes(x = null_dist_stat)) +
  geom_histogram(binwidth = 2, color = "darkblue", fill = "skyblue") + 
  labs(x = "Price per night", y = "Count") +
    geom_vline(xintercept = mean(boot_means$null_dist_stat), lwd = 2, color = "red")
```

---

## Distribution of `$\bar{x}$` under `$H_0$`

---

## Simulating the null distribution with infer

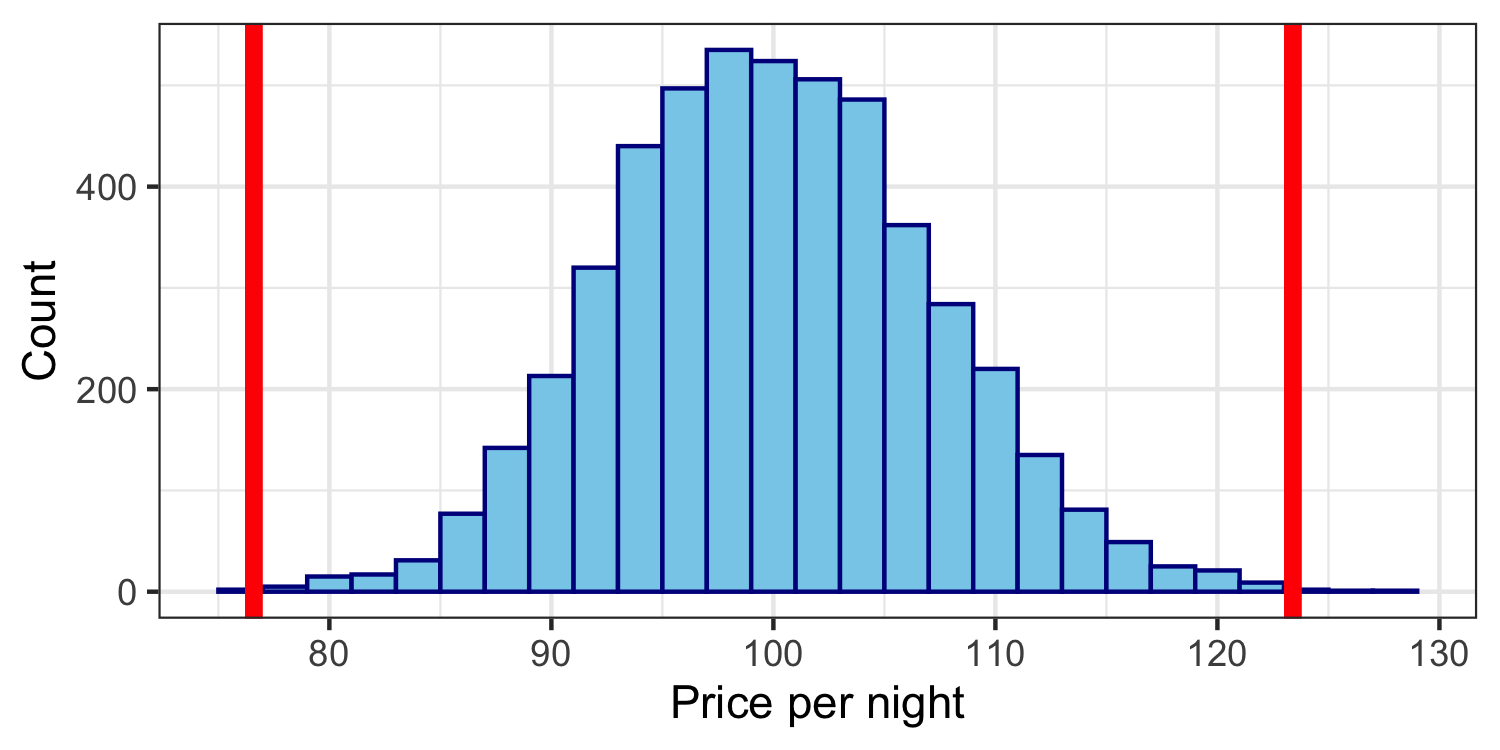
```r
null_dist <- asheville %>%
  specify(response = ppg) %>%
  hypothesize(null = "point", mu = 100) %>%
* generate(reps = 5000, type = "bootstrap") %>%
  calculate(stat = "mean")
```

```r
null_dist
```

```
## # A tibble: 5,000 x 2
##    replicate  stat
##        <int> <dbl>
##  1         1 104. 
##  2         2 112. 
##  3         3  92.7
##  4         4 102. 
##  5         5  93.8
##  6         6 123. 
##  7         7 104. 
##  8         8 109. 
##  9         9 106. 
## 10        10 102. 
## # … with 4,990 more rows
```
]

```r
null_dist %>%
  summarise(mean = mean(stat))
```

```
## # A tibble: 1 x 1
##    mean
##   <dbl>
## 1  100.
```
]

---

## 3️⃣ Assessing the evidence

---

## 3️⃣ Assessing the evidence

```r
null_dist %>%
  filter(stat <= 76.6 | stat >= (100 + (100 - 76.6))) %>%
  summarise(p_value = n()/nrow(null_dist))
```

```
## # A tibble: 1 x 1
##   p_value
##     <dbl>
## 1  0.0008
```

---

## 4️⃣ Make conclusion

The p-value, 0.0008 is less than 0.05, so we .vocab[reject `$H_0$`]. The data provide sufficient evidence that the mean price per guest per night for Airbnbs in Asheville is not equal to $100.

---

## Discussion questions

- `$H_a$` here was a .vocab[two-sided] hypothesis `$(H_a: \mu \neq 100)$`. How does this compare to the .vocab[one-sided] hypothesis from last time `$(H_a: p < 0.1)$`?

- How might the p-value change depending on what type of alternative hypothesis
is specified?

- Why did we need to "shift" the bootstrap distribution when we generated the null distribution in this example, but we didn't need shift the distribution last time when we  generated the null distribution for inference on the population proportion?