Multiple linear regression
Prof. Maria Tackett
Review
Vocabulary
Vocabulary
- Response variable: Variable whose behavior or variation you are trying to understand.
Vocabulary
Response variable: Variable whose behavior or variation you are trying to understand.
Explanatory variables: Other variables that you want to use to explain the variation in the response.
Vocabulary
Response variable: Variable whose behavior or variation you are trying to understand.
Explanatory variables: Other variables that you want to use to explain the variation in the response.
Predicted value: Output of the model function
- The model function gives the typical value of the response variable conditioning on the explanatory variables.
Vocabulary
Response variable: Variable whose behavior or variation you are trying to understand.
Explanatory variables: Other variables that you want to use to explain the variation in the response.
Predicted value: Output of the model function
- The model function gives the typical value of the response variable conditioning on the explanatory variables.
- Residuals: Shows how far each case is from its predicted value
- Residual = Observed value - Predicted value
The linear model with a single predictor
- We're interested in the β0 (population parameter for the intercept) and the β1 (population parameter for the slope) in the following model:
ˆy=β0+β1 x
The linear model with a single predictor
- We're interested in the β0 (population parameter for the intercept) and the β1 (population parameter for the slope) in the following model:
ˆy=β0+β1 x
Unfortunately, we can't get these values
So we use sample statistics to estimate them:
ˆy=b0+b1 x
Least squares regression
The regression line minimizes the sum of squared residuals.
Residuals: ei=yi−ˆyi,
The regression line minimizes ∑ni=1e2i.
Equivalently, minimizing ∑ni=1[yi−(b0+b1 xi)]2
Data and Packages
library(tidyverse)library(broom)paris_paintings <- read_csv("data/paris_paintings.csv", na = c("n/a", "", "NA"))- Paris Paintings Codebook
- Source: Printed catalogues from 28 auction sales held in Paris 1764 - 1780
- 3,393 paintings, prices, descriptive details, characteristics of the auction and buyer (over 60 variables)
Single numerical predictor
m_ht_wd <- lm(Height_in ~ Width_in, data = paris_paintings)tidy(m_ht_wd)## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 3.62 0.254 14.3 8.82e-45## 2 Width_in 0.781 0.00950 82.1 0.^Heightin=3.62+0.78 Widthin
Single categorical predictor (2 levels)
m_ht_lands <- lm(Height_in ~ factor(landsALL), data = paris_paintings)tidy(m_ht_lands)## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 22.7 0.328 69.1 0. ## 2 factor(landsALL)1 -5.65 0.532 -10.6 7.97e-26^Heightin=22.68−5.65 landsALL
Single categorical predictor (> 2 levels)
m_ht_sch <- lm(Height_in ~ school_pntg, data = paris_paintings)tidy(m_ht_sch)## # A tibble: 7 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 14. 10.0 1.40 0.162 ## 2 school_pntgD/FL 2.33 10.0 0.232 0.816 ## 3 school_pntgF 10.2 10.0 1.02 0.309 ## 4 school_pntgG 1.65 11.9 0.139 0.889 ## 5 school_pntgI 10.3 10.0 1.02 0.306 ## 6 school_pntgS 30.4 11.4 2.68 0.00744## 7 school_pntgX 2.87 10.3 0.279 0.780^Heightin=14+2.33 schD/FL+10.2 schF+1.65 schG+10.3 schI+30.4 schS+2.87 schX
The linear model with multiple predictors
The linear model with multiple predictors
- Population model:
ˆy=β0+β1 x1+β2 x2+⋯+βk xk
The linear model with multiple predictors
- Population model:
ˆy=β0+β1 x1+β2 x2+⋯+βk xk
- Sample model that we use to estimate the population model:
ˆy=b0+b1 x1+b2 x2+⋯+bk xk
Data
The data set contains prices for Porsche and Jaguar cars for sale on cars.com.
car: car make (Jaguar or Porsche)
price: price in USD
age: age of the car in years
mileage: previous miles driven
Price, age, and make
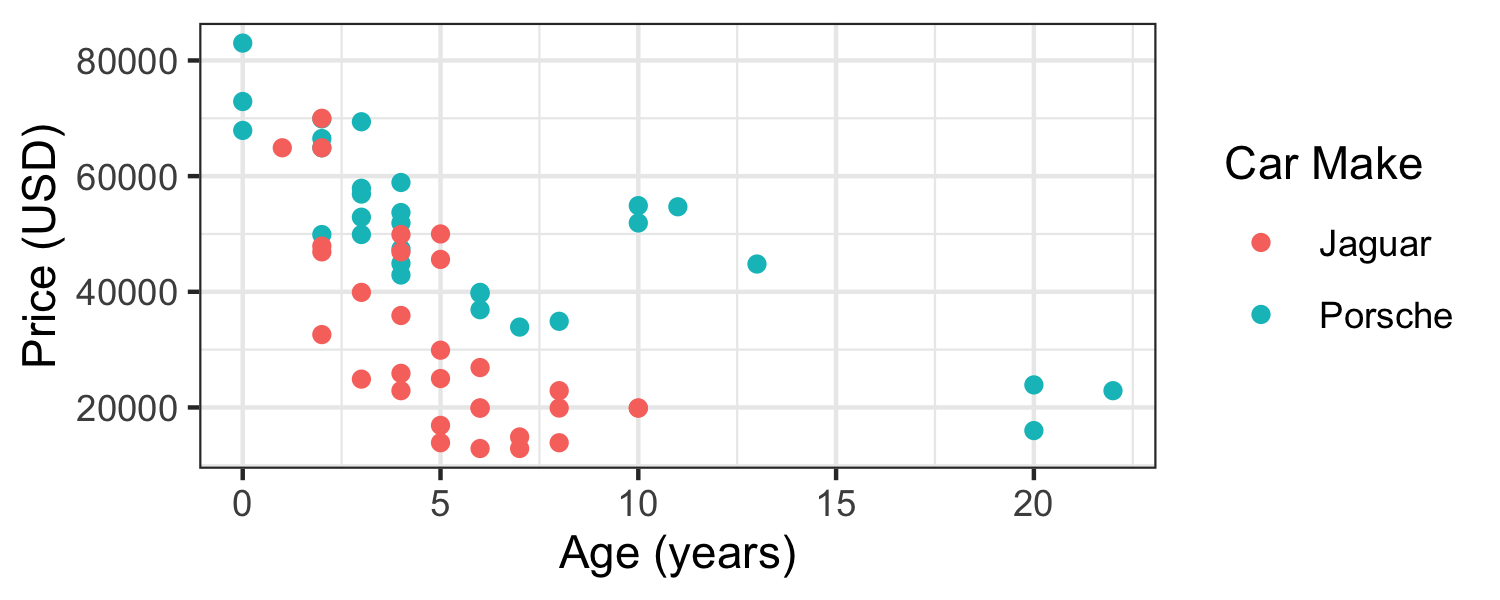
Price vs. age and make
Does the relationship between age and price depend on the make of the car?
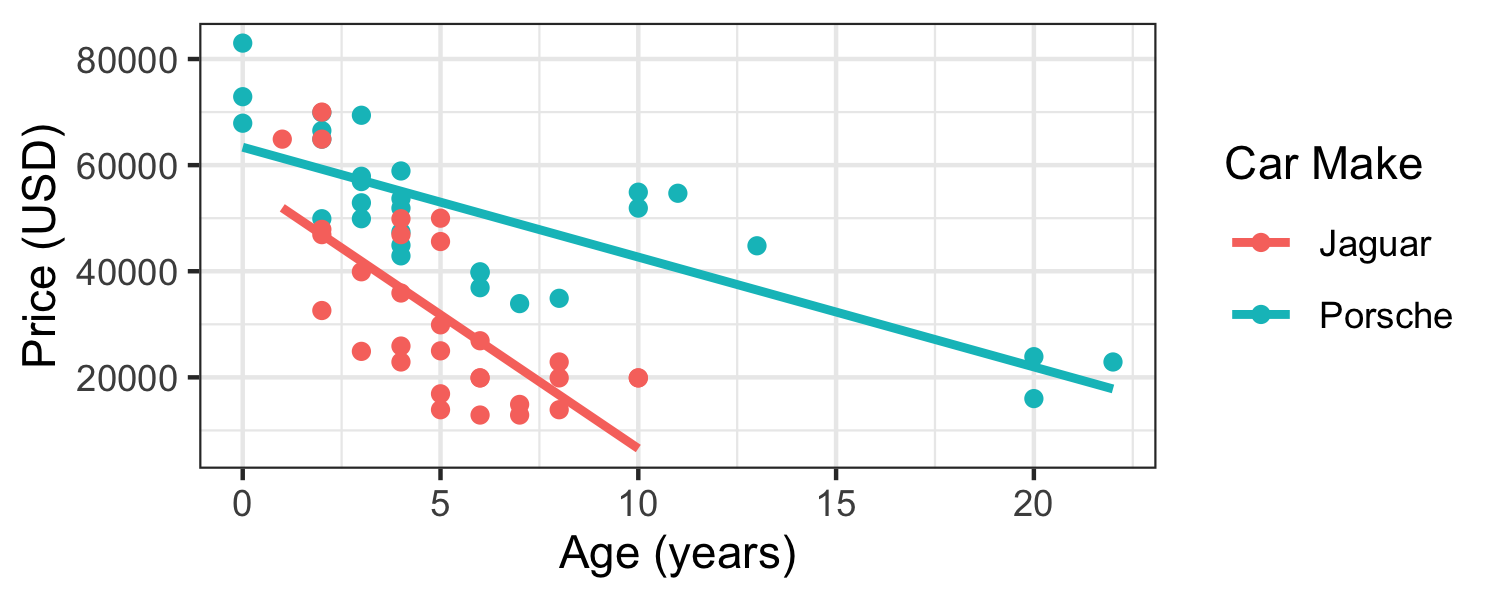
Modeling with main effects
m_main <- lm(price ~ age + car, data = sports_car_prices)m_main %>% tidy() %>% select(term, estimate)## # A tibble: 3 x 2## term estimate## <chr> <dbl>## 1 (Intercept) 44310.## 2 age -2487.## 3 carPorsche 21648.Modeling with main effects
m_main <- lm(price ~ age + car, data = sports_car_prices)m_main %>% tidy() %>% select(term, estimate)## # A tibble: 3 x 2## term estimate## <chr> <dbl>## 1 (Intercept) 44310.## 2 age -2487.## 3 carPorsche 21648.^price=44310−2487 age+21648 carPorsche
^price=44310−2487 age+21648 carPorsche
- Plug in 0 for
carPorscheto get the linear model for Jaguars.
^price=44310−2487 age+21648 carPorsche
- Plug in 0 for
carPorscheto get the linear model for Jaguars.
^price=44310−2487 age+21648×0=44310−2487 age
^price=44310−2487 age+21648 carPorsche
- Plug in 0 for
carPorscheto get the linear model for Jaguars.
^price=44310−2487 age+21648×0=44310−2487 age
- Plug in 1 for
carPorscheto get the linear model for Porsches.
^price=44310−2487 age+21648 carPorsche
- Plug in 0 for
carPorscheto get the linear model for Jaguars.
^price=44310−2487 age+21648×0=44310−2487 age
- Plug in 1 for
carPorscheto get the linear model for Porsches.
^price=44310−2487 age+21648×1=65958−2487 age
Jaguar
^price=44310−2487 age+21648×0=44310−2487 age
Porsche
^price=44310−2487 age+21648×1=65958−2487 age
- Rate of change in price as the age of the car increases does not depend on make of car (same slopes)
- Porsches are consistently more expensive than Jaguars (different intercepts)
Interpretation of main effects
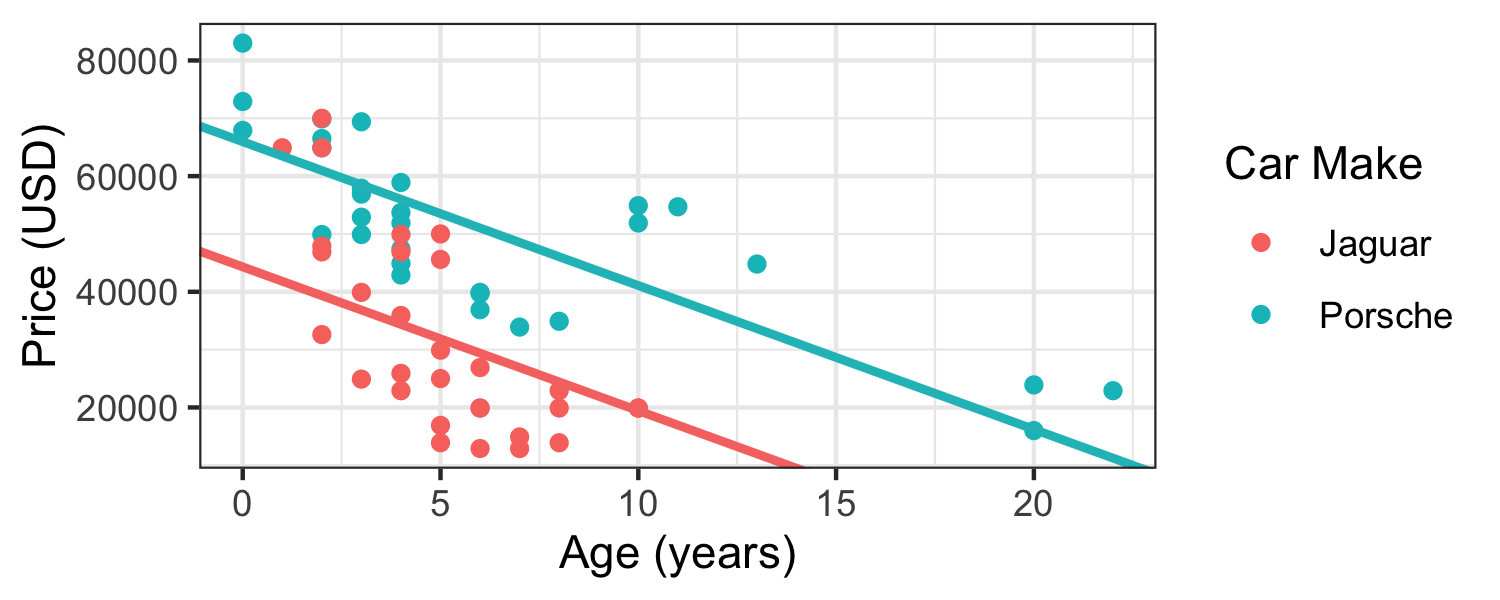
Main effects
## # A tibble: 3 x 2## term estimate## <chr> <dbl>## 1 (Intercept) 44310.## 2 age -2487.## 3 carPorsche 21648.Main effects
## # A tibble: 3 x 2## term estimate## <chr> <dbl>## 1 (Intercept) 44310.## 2 age -2487.## 3 carPorsche 21648.- All else held constant, for each additional year of a car's age, the price of the car is predicted to decrease, on average, by $2,487.
Main effects
## # A tibble: 3 x 2## term estimate## <chr> <dbl>## 1 (Intercept) 44310.## 2 age -2487.## 3 carPorsche 21648.All else held constant, for each additional year of a car's age, the price of the car is predicted to decrease, on average, by $2,487.
All else held constant, Porsches are predicted, on average, to have a price that is $21,647 greater than Jaguars.
Main effects
## # A tibble: 3 x 2## term estimate## <chr> <dbl>## 1 (Intercept) 44310.## 2 age -2487.## 3 carPorsche 21648.All else held constant, for each additional year of a car's age, the price of the car is predicted to decrease, on average, by $2,487.
All else held constant, Porsches are predicted, on average, to have a price that is $21,647 greater than Jaguars.
Jaguars that are new (age = 0) are predicted, on average, to have a price of $44,309.
Why is our linear regression model different from what we got from geom_smooth(method = "lm")?
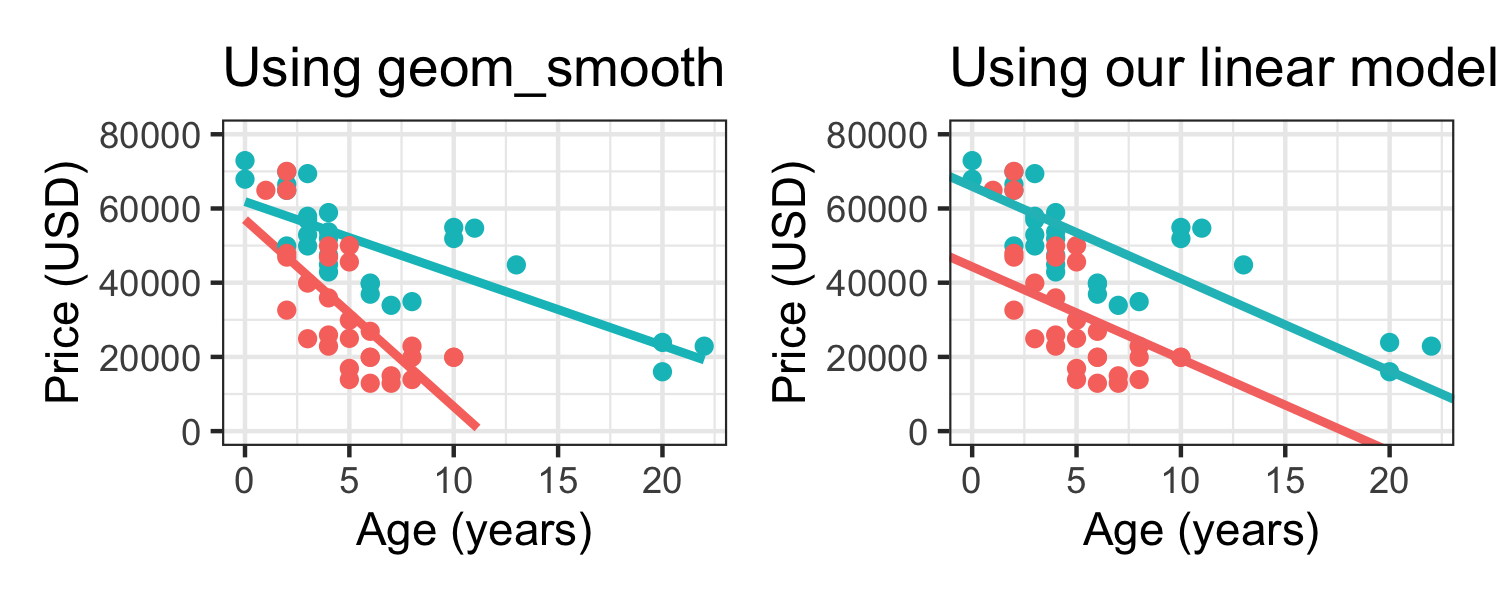
What went wrong?
What went wrong?
caris the only variable in our model that affects the intercept.
What went wrong?
caris the only variable in our model that affects the intercept.The model we specified assumes Jaguars and Porsches have the
same slopeanddifferent intercepts.
What went wrong?
caris the only variable in our model that affects the intercept.The model we specified assumes Jaguars and Porsches have the
same slopeanddifferent intercepts.What is the most appropriate model for these data?
- same slope and intercept for Jaguars and Porsches?
- same slope and different intercept for Jaguars and Porsches?
- different slope and different intercept for Jaguars and Porsches?
Interacting explanatory variables
Including an interaction effect in the model allows for different slopes, i.e. nonparallel lines.
This means that the relationship between an explanatory variable and the response depends on another explanatory variable.
We can accomplish this by adding an interaction variable. This is the product of two explanatory variables.
Price vs. age and car interacting
ggplot(data = sports_car_prices, mapping = aes(y = price, x = age, color = car)) + geom_point() + geom_smooth(method = "lm", se = FALSE) + labs(x = "Age (years)", y = "Price (USD)", color = "Car Make")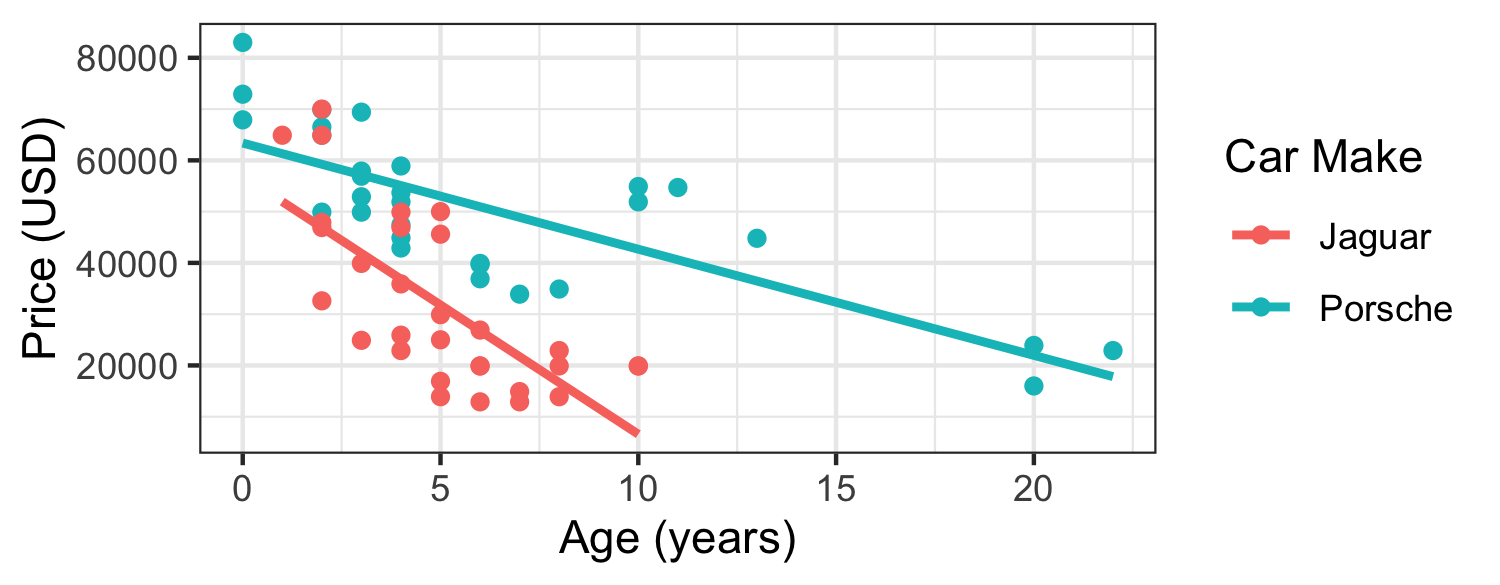
Modeling with interaction effects
m_int <- lm(price ~ age + car + age * car, data = sports_car_prices) m_int %>% tidy() %>% select(term, estimate)## # A tibble: 4 x 2## term estimate## <chr> <dbl>## 1 (Intercept) 56988.## 2 age -5040.## 3 carPorsche 6387.## 4 age:carPorsche 2969.^price=56988−5040 age+6387 carPorsche+2969 age×carPorsche
Interpretation of interaction effects
^price=56988−5040 age+6387 carPorsche+2969 age×carPorsche
Interpretation of interaction effects
^price=56988−5040 age+6387 carPorsche+2969 age×carPorsche
- Plug in 0 for
carPorscheto get the linear model for Jaguars.
^price=56988−5040 age+6387 carPorsche+2969 age×carPorsche=56988−5040 age+6387×0+2969 age×0=56988−5040 age
Interpretation of interaction effects
^price=56988−5040 age+6387 carPorsche+2969 age×carPorsche
- Plug in 0 for
carPorscheto get the linear model for Jaguars.
^price=56988−5040 age+6387 carPorsche+2969 age×carPorsche=56988−5040 age+6387×0+2969 age×0=56988−5040 age
- Plug in 1 for
carPorscheto get the linear model for Porsches.
^price=56988−5040 age+6387 carPorsche+2969 age×carPorsche=56988−5040 age+6387×1+2969 age×1=63375−2071 age
Interpretation of interaction effects
Jaguar
^price=56988−5040 age
Porsche
^price=63375−2071 age
Rate of change in price as the age of the car increases depends on the make of the car (different slopes).
Porsches are consistently more expensive than Jaguars (different intercepts).
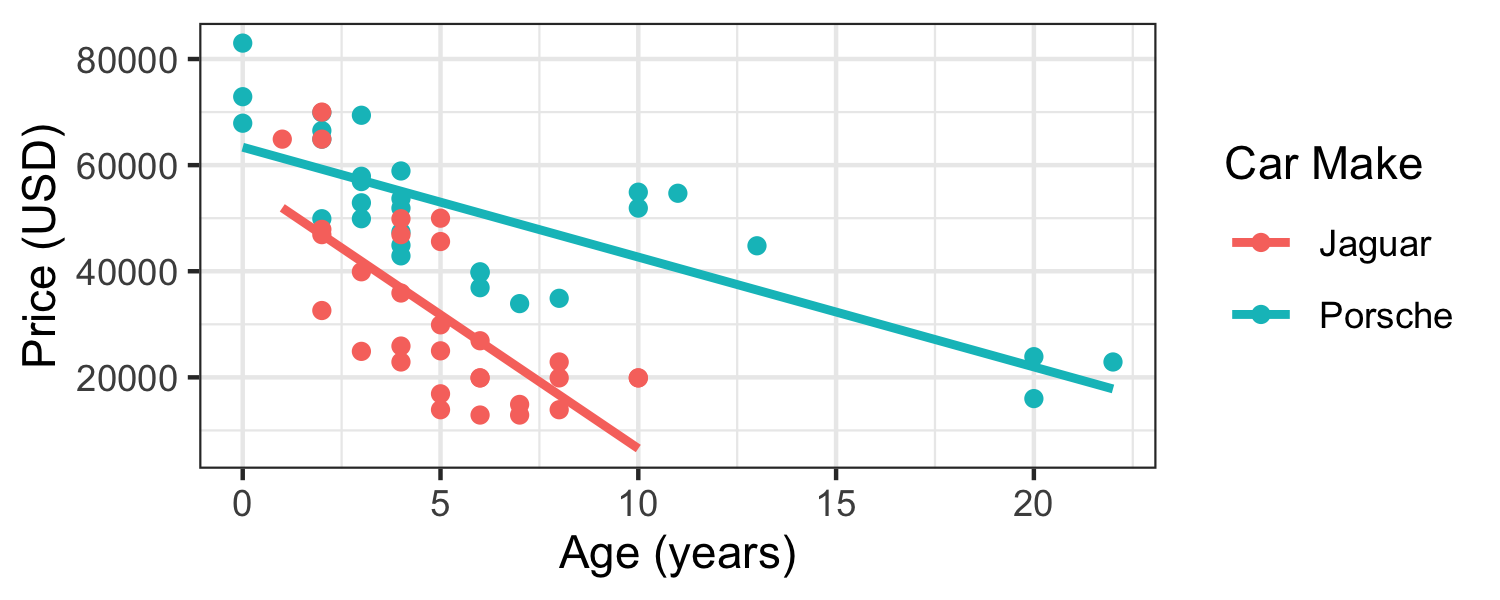
^price=56988−5040 age+6387 carPorsche+2969 age×carPorsche
Continuous by continuous interactions
Interpretation becomes trickier
Slopes conditional on values of explanatory variables
Continuous by continuous interactions
Interpretation becomes trickier
Slopes conditional on values of explanatory variables
Third order interactions
Can you? Yes
Should you? Probably not if you want to interpret these interactions in context of the data.
Assessing quality of model fit
Assessing the quality of the fit
The strength of the fit of a linear model is commonly evaluated using R2.
It tells us what percentage of the variability in the response variable is explained by the model. The remainder of the variability is unexplained.
R2 is sometimes called the coefficient of determination.
What does "explained variability in the response variable" mean?
Obtaining R2 in R
price vs. age and make
glance(m_main)## # A tibble: 1 x 12## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 0.607 0.593 11848. 44.0 2.73e-12 2 -646. 1301. 1309.## # … with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>glance(m_main)$r.squared## [1] 0.6071375Obtaining R2 in R
price vs. age and make
glance(m_main)## # A tibble: 1 x 12## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 0.607 0.593 11848. 44.0 2.73e-12 2 -646. 1301. 1309.## # … with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>glance(m_main)$r.squared## [1] 0.6071375About 60.7% of the variability in price of used cars can be explained by age and make.
R2
glance(m_main)$r.squared #model with main effects## [1] 0.6071375glance(m_int)$r.squared #model with main effects + interactions## [1] 0.6677881R2
glance(m_main)$r.squared #model with main effects## [1] 0.6071375glance(m_int)$r.squared #model with main effects + interactions## [1] 0.6677881- The model with interactions has a higher R2.
R2
glance(m_main)$r.squared #model with main effects## [1] 0.6071375glance(m_int)$r.squared #model with main effects + interactions## [1] 0.6677881The model with interactions has a higher R2.
Using R2 for model selection in models with multiple explanatory variables is not a good idea as R2 increases when any variable is added to the model.
R2 - first principles
- We can write explained variation using the following ratio of sums of squares:
R2=1−(variability in residualsvariability in response)
Why does this expression make sense?
- But remember, adding any explanatory variable will always increase R2
Adjusted R2
R2adj=1−(variability in residualsvariability in response×n−1n−k−1)
Adjusted R2
R2adj=1−(variability in residualsvariability in response×n−1n−k−1)
- Adjusted R2 doesn't increase if the new variable does not provide any new information or is completely unrelated.
Adjusted R2
R2adj=1−(variability in residualsvariability in response×n−1n−k−1)
Adjusted R2 doesn't increase if the new variable does not provide any new information or is completely unrelated.
This makes adjusted R2 a preferable metric for model selection in multiple regression models.
Comparing models
glance(m_main)$r.squared## [1] 0.6071375glance(m_int)$r.squared## [1] 0.6677881glance(m_main)$adj.r.squared## [1] 0.5933529glance(m_int)$adj.r.squared## [1] 0.649991In pursuit of Occam's Razor
Occam's Razor states that among competing hypotheses that predict equally well, the one with the fewest assumptions should be selected.
Model selection follows this principle.
We only want to add another variable to the model if the addition of that variable brings something valuable in terms of predictive power to the model.
In other words, we prefer the simplest best model, i.e. parsimonious model.