Vocabulary

• Response variable: Variable whose behavior or variation you are trying to understand.

• Explanatory variables: Other variables that you want to use to explain the variation in the response.

• Predicted value: Output of the model function

• Residuals: Shows how far each case is from its predicted value

  • Residual = Observed value - Predicted value

The linear model with multiple predictors

• Population model:

ˆy=β0+β1 x1+β2 x2+⋯+βk xk

• Sample model that we use to estimate the population model:

ˆy=b0+b1 x1+b2 x2+⋯+bk xk

Data and Packages

library(tidyverse)
library(broom)

Recall the file sportscars.csv contains prices for Porsche and Jaguar cars for sale on cars.com.

car: car make (Jaguar or Porsche)

price: price in USD

age: age of the car in years

mileage: previous miles driven

Multiple Linear Regression

m_int <- lm(price ~ age + car + age * car, 
            data = sports_car_prices) 
m_int %>%
  tidy() %>%
  select(term, estimate)

## # A tibble: 4 x 2
##   term           estimate
##   <chr>             <dbl>
## 1 (Intercept)      56988.
## 2 age              -5040.
## 3 carPorsche        6387.
## 4 age:carPorsche    2969.

^price=56988−5040 age+6387 carPorsche+2969 age×carPorsche

The linear model with multiple predictors

Population model:

ˆy=β0+β1 x1+β2 x2+⋯+βk xk

Sample model that we use to estimate the population model:

ˆy=b0+b1 x1+b2 x2+⋯+bk xk

Similar to other sample statistics (mean, proportion, etc) there is variability in our estimates of the slope and intercept.

Mileage vs. age

We will consider a simple linear regression model predicting mileage using age.

m_age_miles <- lm(mileage ~ age, data = sports_car_prices)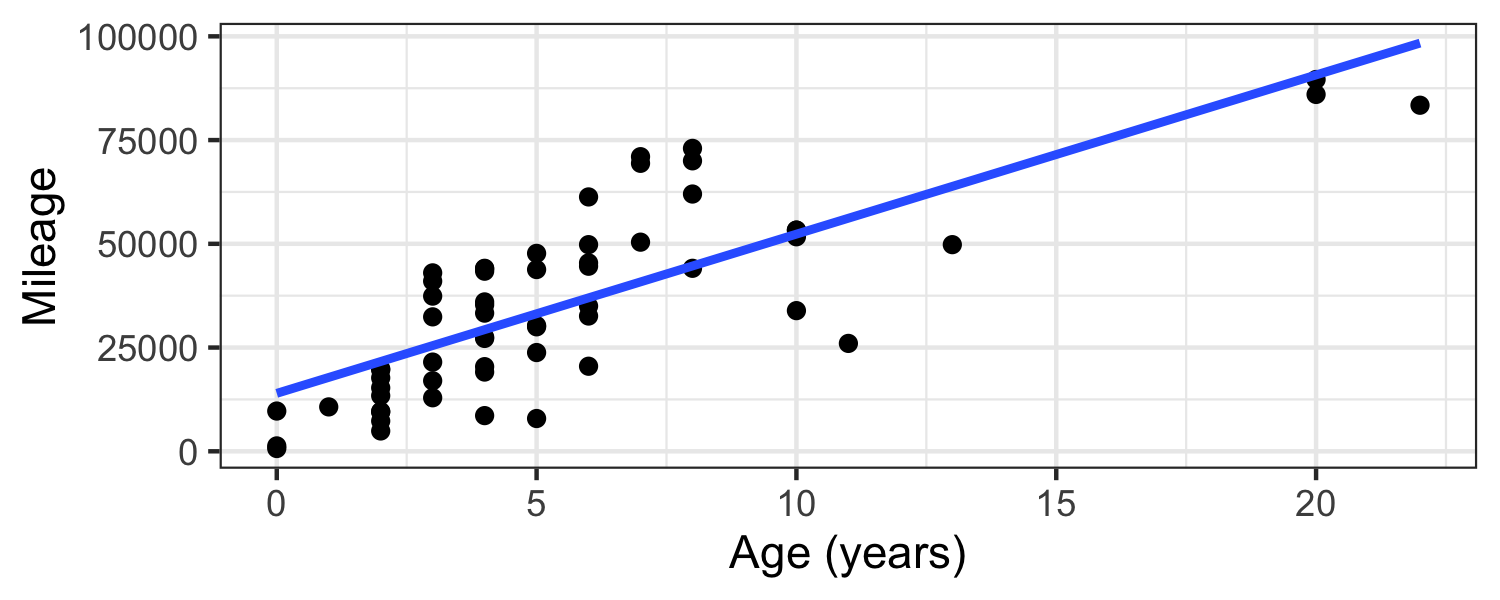

Confidence interval

Tidy confidence interval

tidy(m_age_miles, conf.int = TRUE, conf.level = 0.95)

## # A tibble: 2 x 7
##   term        estimate std.error statistic  p.value conf.low conf.high
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
## 1 (Intercept)   13967.     2876.      4.86 9.40e- 6    8211.    19723.
## 2 age            3837.      403.      9.52 1.86e-13    3030.     4643.

Calculating the 95% CI manually

A 95% confidence interval for β1 can be calculated as

(df <- nrow(sports_car_prices) - 2)

## [1] 58

(tstar <- qt(0.975,df))

## [1] 2.001717

(ci <- 3837 + c(-1,1) * tstar *403)

## [1] 3030.308 4643.692

Interpretation

tidy(m_age_miles, conf.int = TRUE, conf.level = 0.95) %>% 
  filter(term == "age") %>%
  select(conf.low, conf.high)

## # A tibble: 1 x 2
##   conf.low conf.high
##      <dbl>     <dbl>
## 1    3030.     4643.

Hypothesis testing for β1

Is there convincing evidence, based on our sample data, that age is associated with mileage?

We can set this up as a hypothesis test, with the hypotheses below.

We only reject H0 in favor of Ha if the data provide strong evidence that the true slope parameter is different from zero.

Hypothesis testing for β1

tidy(m_age_miles)

## # A tibble: 2 x 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)   13967.     2876.      4.86 9.40e- 6
## 2 age            3837.      403.      9.52 1.86e-13

T=b1−0SEb1∼tn−2

The p-value is in the output is the p-value associated with the two-sided hypothesis test Ha:β1≠0.

Hypothesis testing for β1

tidy(m_age_miles)

## # A tibble: 2 x 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)   13967.     2876.      4.86 9.40e- 6
## 2 age            3837.      403.      9.52 1.86e-13

The p-value is very small, so we reject H0. The data provide sufficient evidence that the coefficient of age is not equal to 0, and there is a linear relationship between the mileage and age of a car.

Final Thoughts

We used a CLT-based approach to construct confidence intervals and perform hypothesis tests.

Note that you can also use simulation-based methods to do inference using infer. Click here for examples.

Conditions

• Linearity: The relationship between response and predictor(s) is linear

• Independence: The residuals are independent

• Normality: The residuals are nearly normally distributed

• Equal Variance: The residuals have constant variance

Conditions

• Linearity: The relationship between response and predictor(s) is linear

• Independence: The residuals are independent

• Normality: The residuals are nearly normally distributed

• Equal Variance: The residuals have constant variance

For multiple regression, the predictors shouldn't be too correlated with each other.

augment data with model results

• .fitted: Predicted value of the response variable
• .resid: Residuals

m_age_miles_aug <- augment(m_age_miles)
m_age_miles_aug %>%
  slice(1:3)

## # A tibble: 3 x 8
##   mileage   age .fitted .resid .std.resid   .hat .sigma  .cooksd
##     <dbl> <dbl>   <dbl>  <dbl>      <dbl>  <dbl>  <dbl>    <dbl>
## 1   21500     3  25477. -3977.     -0.290 0.0223 13981. 0.000959
## 2   43000     3  25477. 17523.      1.28  0.0223 13793. 0.0186  
## 3   19900     2  21640. -1740.     -0.127 0.0275 13989. 0.000229

We will use the fitted values and residuals to check the conditions by constructing diagnostic plots.

Residuals vs fitted plot

Use to check Linearity and Equal variance.

ggplot(m_age_miles_aug, mapping = aes(x = .fitted, y = .resid)) +
  geom_point() + geom_hline(yintercept = 0, lwd = 2, col = "red", lty = 2) +
  labs(x = "Predicted Mileage", y = "Residuals")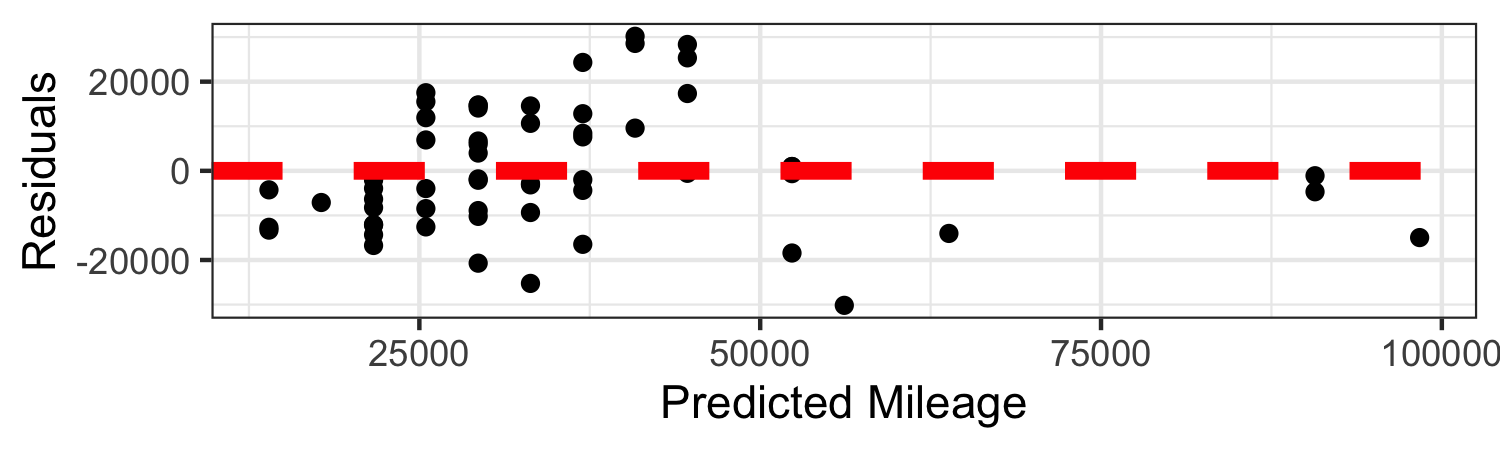

Residuals in order of collection

Use to check Independence

ggplot(data = m_age_miles_aug, 
       aes(x = 1:nrow(sports_car_prices), 
           y = .resid)) + 
  geom_point() + geom_hline(yintercept = 0, lwd = 2, col = "red", lty = 2) +
  labs(x = "Index", y = "Residual")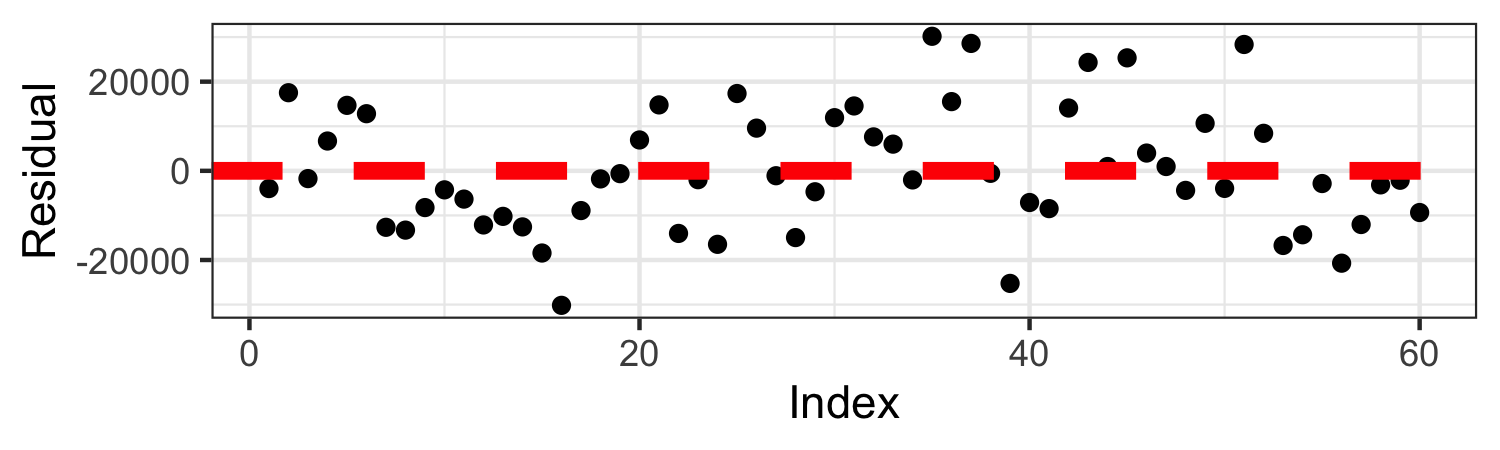

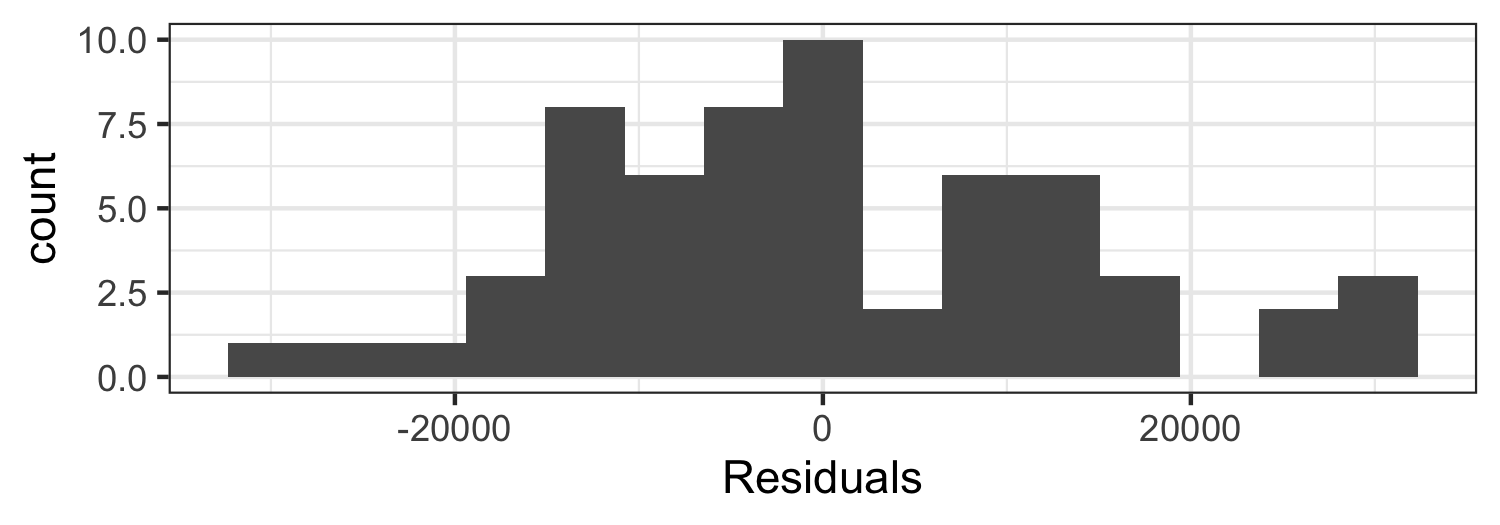
Histogram of residuals

Use to check Normality

ggplot(m_age_miles_aug, mapping = aes(x = .resid)) +
  geom_histogram(bins = 15) + labs(x = "Residuals")